Hoofdstuk 2 Hydrodynamiek
Dit hoofdstuk betreft metingen van de waterbeweging in de Westerschelde en de monding. De rapportage wordt hierbij beperkt tot waterstanden en golven. De waterstanden zijn opgenomen als jaargemiddelde hoog- en laagwaterstanden en de gemiddelde getijslag. Daarnaast zijn de belangrijkste componenten van het getij (M2, S2 en M4-component) weergegeven. Voor golven worden maandgemiddelden en -maxima van de golfhoogte en -periode gepresenteerd.
2.1 Waterstanden
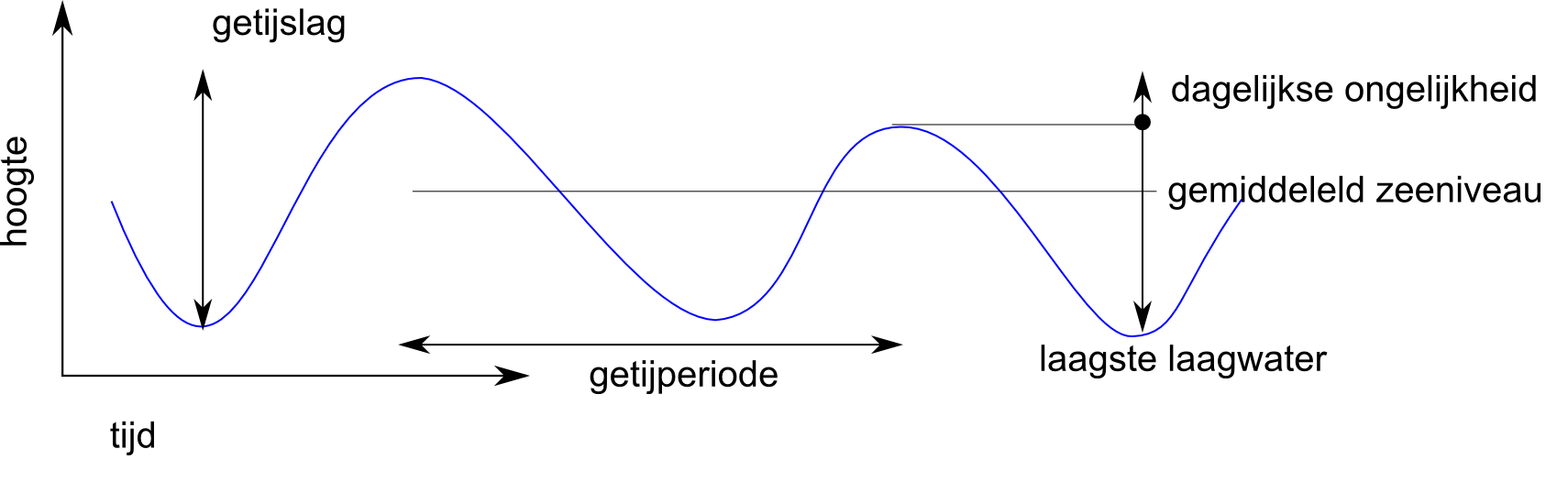
Figuur 2.1: Weergave van een getijgolf met aanduiding hoogwater, laagwater, getijslag en dagelijkse ongelijkheid op basis van Van Rijn (1994).
De waterstanden in de Westerschelde worden voor het grootste deel bepaald door het getij. Het getij ontstaat door de aantrekkende kracht van de maan en de zon op de aarde. De variaties in het getij ontstaan door de draaiing van de aarde en de positie van de aarde t.o.v. de maan en de zon en doordat de maan en de aarde zich in een baan rond de zon bewegen. Daarnaast wordt het getij vervormd door de bodemligging van zeeën en oceanen. Wiskundig gezien is het getij een combinatie van een groot aantal sinusvormige golven: de getijcomponenten. De hoofdcomponent van het getij is de M2-component, die wordt veroorzaakt door de aantrekkingskracht van de maan op de aarde en een periode heeft van ongeveer 12 uur en 25 minuten. De S2 component is een soortgelijke component (een periode van ongeveer 12 uur) maar is gegenereerd door de aantrekkingskracht van de zon op de aarde. De S2-component is samen met M2 verantwoordelijk voor de springtij-doodtij variatie. Hogere harmonische getijcomponenten (zoals M4) worden vaak als ‘overtides’ aangeduid. M4 is het eerste overtide en is gegenereerd door eerste orde niet-lineaire processen. M4 is de eerste hogere harmonische component en is samen met M2 van belang voor sedimenttransport. De belangrijkste periodieke variaties in het getij zorgen voor de zogeheten dagelijkse ongelijkheid (Figuur 2.1), de springtij-doodtij cyclus en de 18,6-jarige cyclus. De 18,6-jarige cyclus wordt veroorzaakt door de afwijking van het baanvlak van de maan ten opzichte van het baanvlak van de aarde (de knopen- of drakencyclus). De invloed van de knopencyclus is sinus-vormig en geeft een verhoging of verlaging van de zeespiegel in een willekeurig jaar van maximaal 13 mm langs de Nederlandse kust. De langjarige trend wordt niet beïnvloed door deze cyclus. Zie Paragraaf 2.1.4 voor meer informatie over de getijden.
Het getij wordt verder vervormd in het estuarium. Vanaf de monding dringt het tij als een langgerekte golf het estuarium binnen. De geringer wordende diepte en vernauwing van de bedding vervormen het getij. Door die versmalling ondergaat het vloedwater een opstuwing; de hoogwaters worden hoger naarmate ze het estuarium dieper binnendringen. Energieverliezen ten gevolge van wrijving doen de verhoging door de opstuwing gedeeltelijk weer teniet. Dit zorgt ervoor dat de symmetrische getijkromme in de monding van de Westerschelde vervormd. Dit wordt getijasymmetrie genoemd. Hierdoor ontstaat er dus een verschil tussen de maximale eb- en vloedsnelheid in het estuarium.
Het gemeten waterstandssignaal kan geanalyseerd worden met een getijanalyse. Hierbij wordt het waterstandssignaal ontleed in verschillende harmonische componenten: sinussen met een zekere amplitude, frequentie en fase. De amplitude en fase van een component verschillen per positie op aarde, de frequentie is altijd gelijk. De amplitude is de uitwijking van de getijcomponent ten opzichte van de middenstand. De fase van de getijcomponent wordt weergegeven ten opzichte van Midden Europese Tijd (MET). Verandering in de fase van een getijcomponent kan van belang zijn voor de interactie met andere getijcomponenten, maar ook voor de looptijd van het getij in het estuarium. Bijvoorbeeld het samenvallen van getijcomponenten zorgt ervoor dat het getij hoger wordt omdat er de krachten elkaar versterken op dat moment. De amplituden en fases van de M2, M4 en S2 componenten worden weergegeven in Figuur 2.21 tot en met 2.26 en in Tabel 2.2.
Tot slot zijn er nog de weersinvloeden zoals wind en luchtdruk. De verschillen in wind en luchtdruk zorgen voor variaties in de waterstanden van jaar op jaar. Waterstanden zijn hoger in stormsituaties waar de windsnelheden toenemen. De windrichting is hierbij van belang. Wind vanaf de Noordzee stuwt het water op het estuarium in. Wind vanaf land stuwt het water het estuarium uit. Dit zorgt ervoor dat de waterstanden bij eb- en vloed hoger of lager worden. In jaren met veel stormen uit westelijke richting op de Noordzee zal de gemiddelde waterstand dus hoger zijn dan in rustige jaren.
2.1.1 Informatie over de metingen
De waterstand in de Westerschelde wordt tegenwoordig continu gemeten op meerdere vaste stations in de Westerschelde. Van deze continue meting wordt een 10-minuten gemiddelde bepaald en opgeslagen in databases. Deze meetreeks wordt gebruikt om o.a. de getijcomponenten te bepalen. Daarnaast worden de maximale hoog- en laagwaterstanden geregistreerd, wat betekent dat ongeveer elke 6 uur een waarde wordt geregistreerd.
De stations zijn zowel landelijke als regionale meetpunten (zie Figuur 2.2, waarvan de meetdata beschikbaar zijn gesteld door het VLIZ (Vlaams Instituut voor de Zee). Alleen voor de landelijke meetpunten wordt een getijanalyse uitgevoerd en daarom worden voor deze stations de getijcomponenten M2, M4 en S2 gerapporteerd.
In Paragraaf 2.1.2 zijn de jaargemiddelde hoog- en laagwaterstanden per station weergegeven. Het verschil tussen de hoog- en laagwaterstanden geeft de gemiddelde getijslag, zie Paragraaf 2.1.3. De meetgegevens zijn niet gecorrigeerd voor de 18,6-jarige cyclus. Tot slot wordt voor de landelijke meetpunten de amplitude en fase van de M2, M4 en S2 getijcomponenten weergegeven in Paragraaf 2.1.4.
Om trends in de waterstanden te kunnen herkennen, wordt de data over een lange periode weergegeven: vanaf 1998 tot heden. Het waterstandsmeetpunt Schaar van de Noord is van 9 juli 2013 tot 25 juni 2015 niet in gebruik geweest.
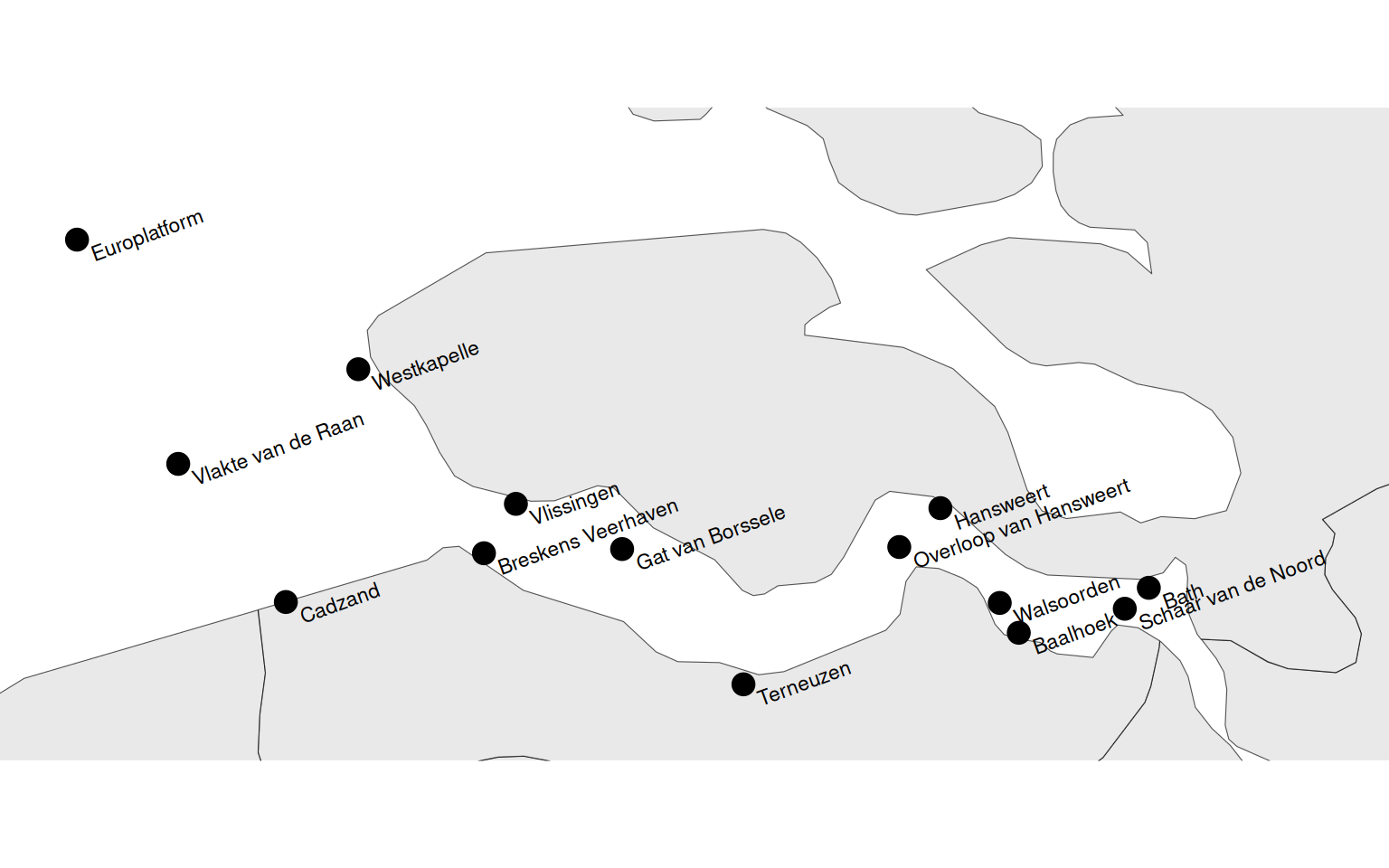
Figuur 2.2: Ligging van de meetstations voor de waterstanden
2.1.2 Jaargemiddelde hoog- en laagwaterstanden
In de grafieken (Figuur 2.3 tot en met Figuur 2.16) onderstaand en op de volgende pagina’s zijn de hoog- en laagwaterstanden ten opzichte van NAP of MSL (Mean Sea Level) per jaar gemiddeld en uitgezet in de tijd. Gemiddelde hoogwaterstanden worden weergegeven in het bovenste gedeelte van de grafiek en gemiddelde laagwaterstanden worden weergegeven in het onderste gedeelte. Voor jaren met missende data voor twee of meer maanden worden de gemiddeldes met lijnen weergegeven. Aan deze gemiddeldes kan minder waarde gehecht worden. De volgorde waarin de stations zijn weergegeven is stroomopwaarts: vanaf het Europlatform in de Noordzee tot de Belgische grens.
Het station Schaar van de Noord heeft voor 2014 geen data. In 2013 is alleen data beschikbaar tot juli 2013, dus slechts ongeveer een half jaar. Het jaar 2013 lijkt voor Schaar van de Noord een lagere waarde te geven (zie Figuur 2.15), maar het kan zijn dat de lengte van de dataset van 2013 dit gemiddelde beïnvloedt. De laatste twee jaren geven waardes die in het verlengde liggen van de jaren voor 2013.
Let op: de y-assen van de figuren verschillen van elkaar.
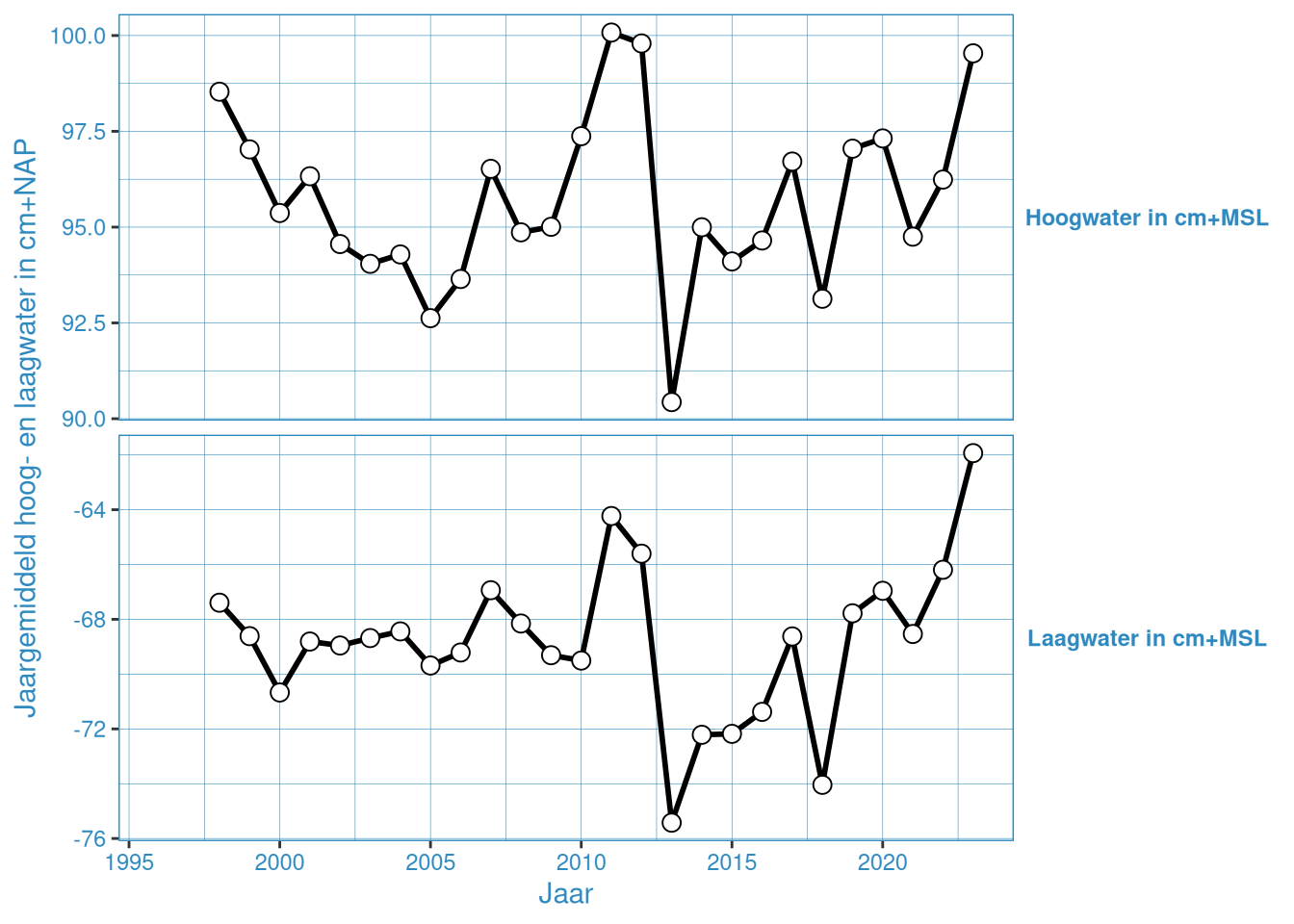
Figuur 2.3: Jaargemiddelde hoog- en laagwaterstanden bij het Europlatform
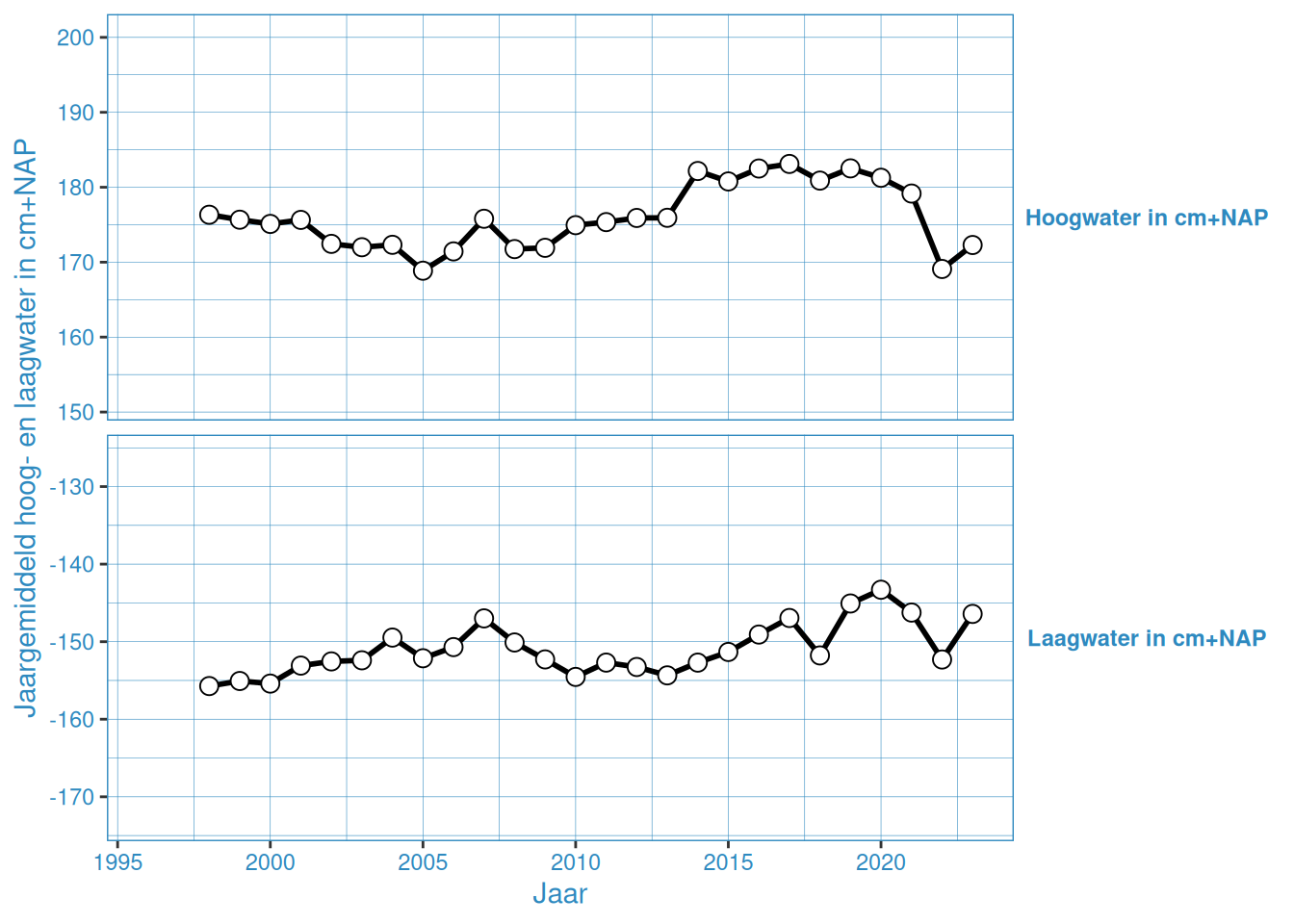
Figuur 2.4: Jaargemiddelde hoog- en laagwaterstanden bij de Vlakte van de Raan
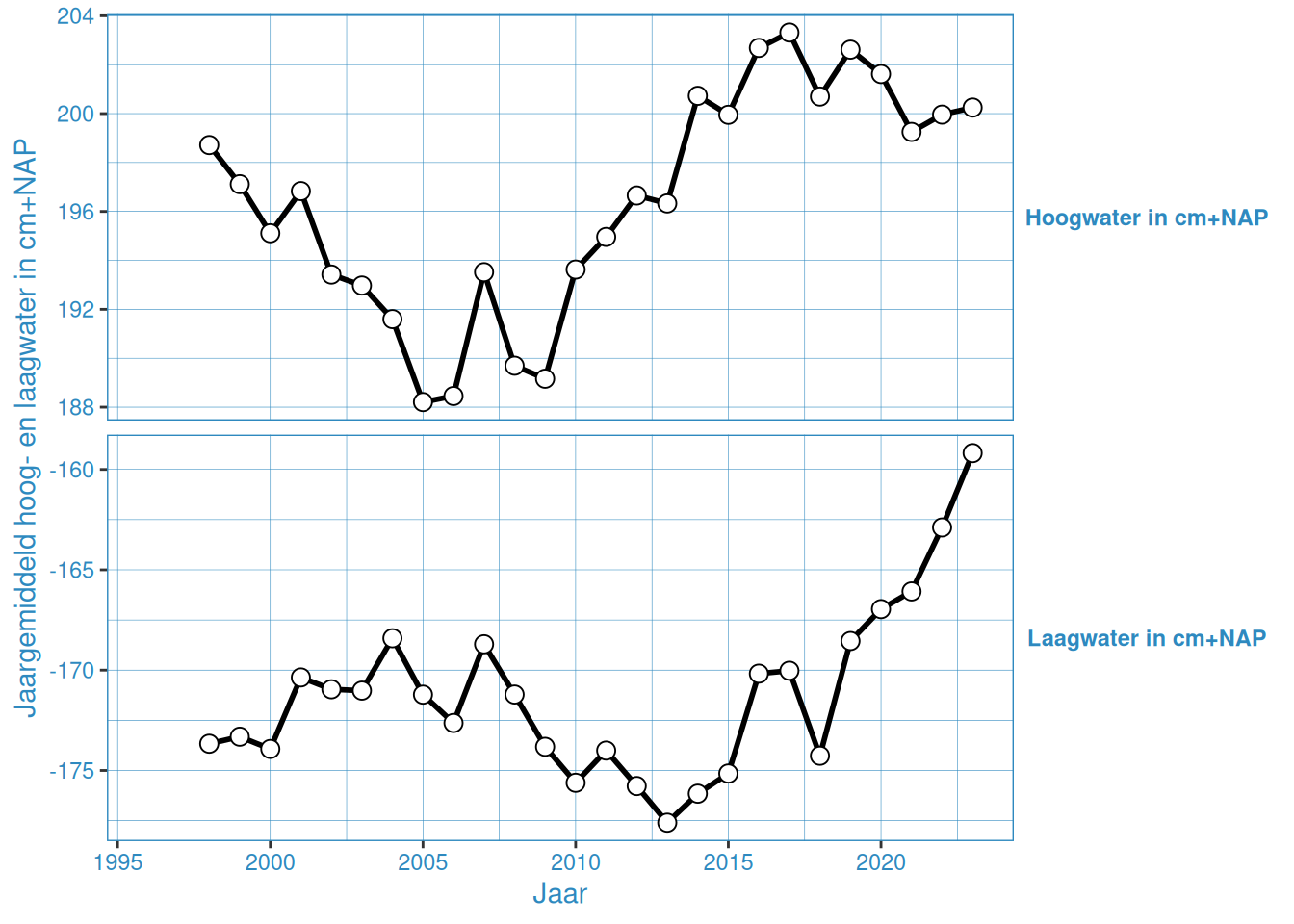
Figuur 2.5: Jaargemiddelde hoog- en laagwaterstanden bij Cadzand
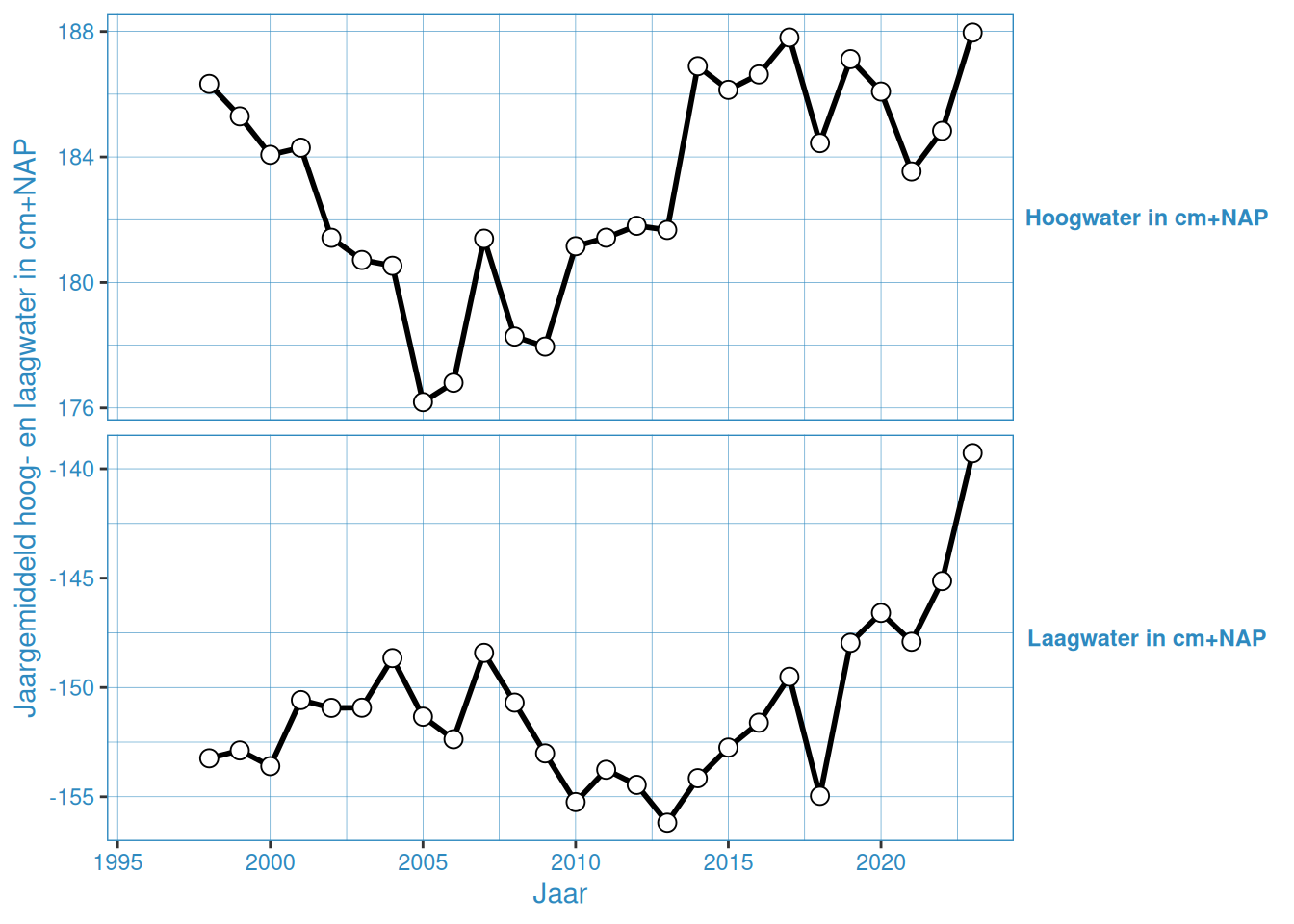
Figuur 2.6: Jaargemiddelde hoog- en laagwaterstanden bij Westkapelle
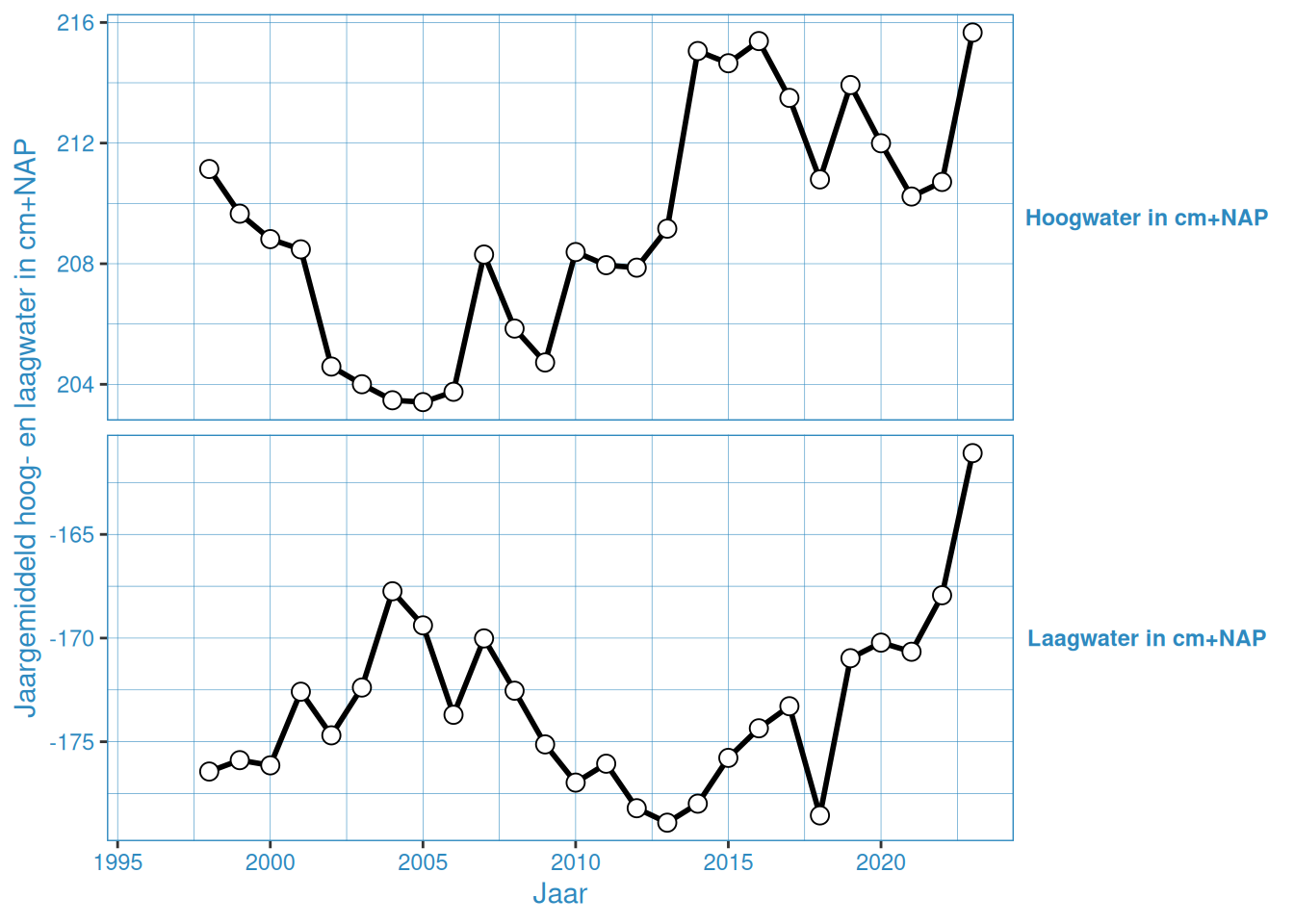
Figuur 2.7: Jaargemiddelde hoog- en laagwaterstanden bij Breskens veerhaven
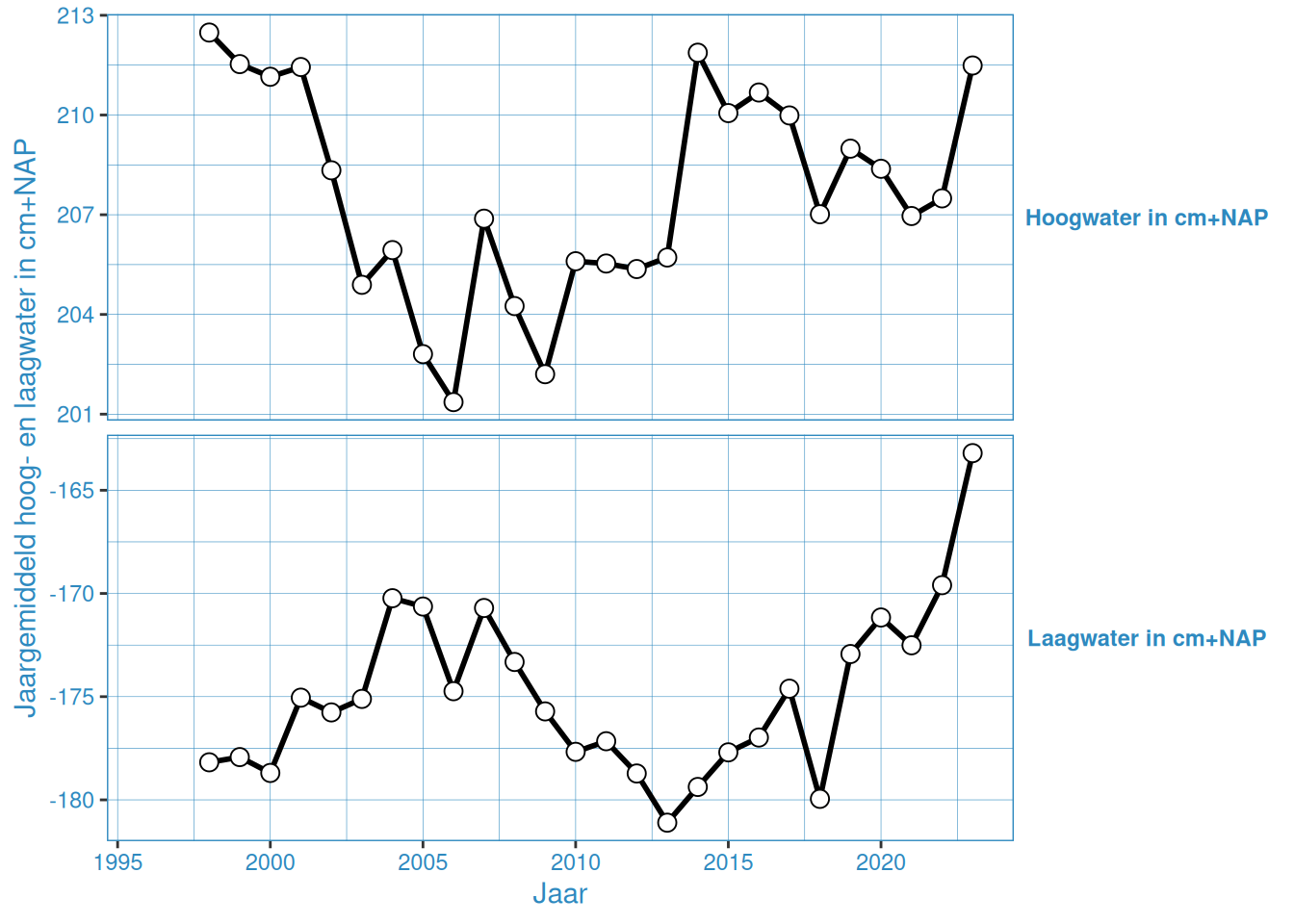
Figuur 2.8: Jaargemiddelde hoog- en laagwaterstanden bij Vlissingen
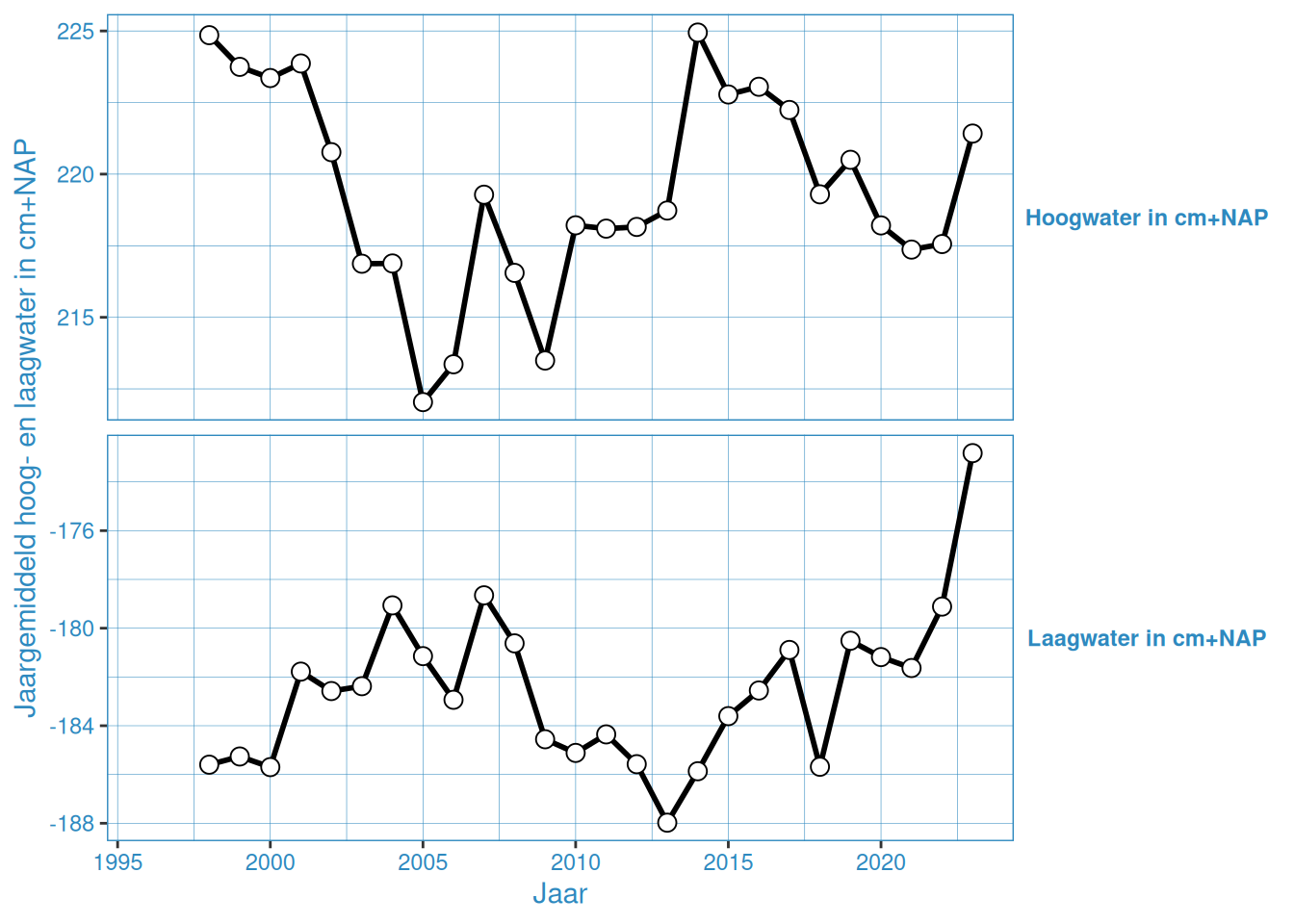
Figuur 2.9: Jaargemiddelde hoog- en laagwaterstanden bij Gat van Borssele
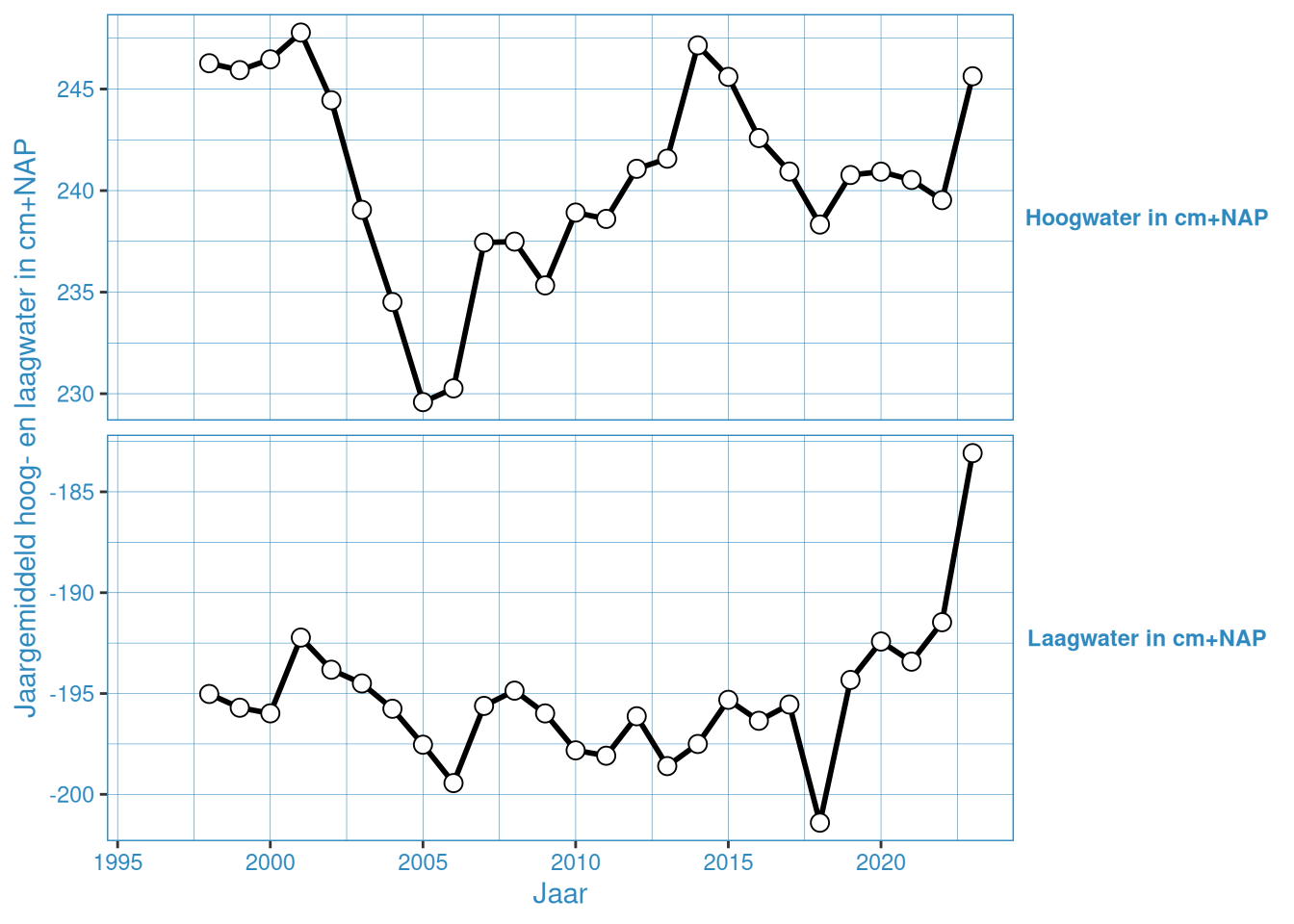
Figuur 2.10: Jaargemiddelde hoog- en laagwaterstanden bij Overloop van Hansweert
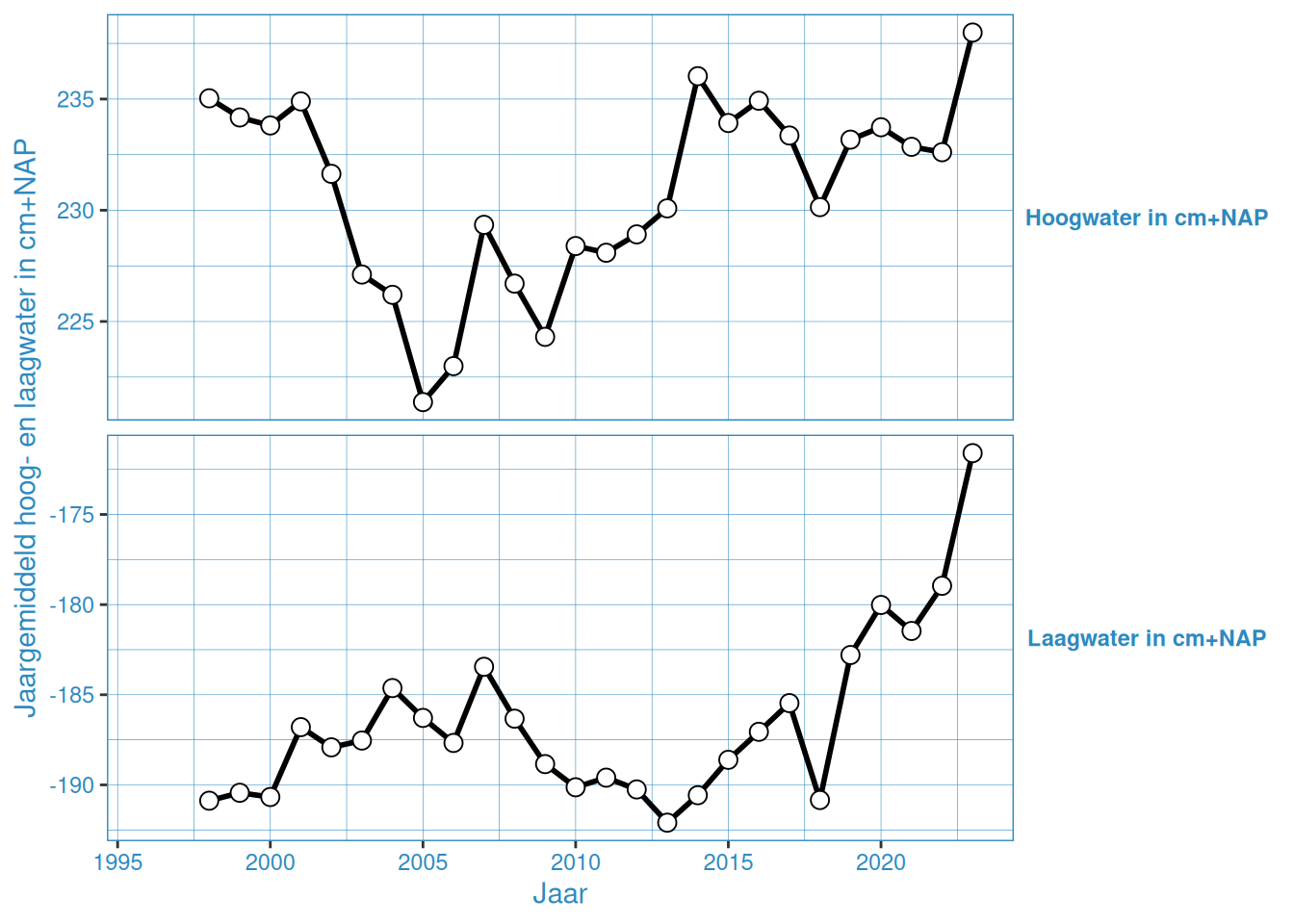
Figuur 2.11: Jaargemiddelde hoog- en laagwaterstanden bij Terneuzen
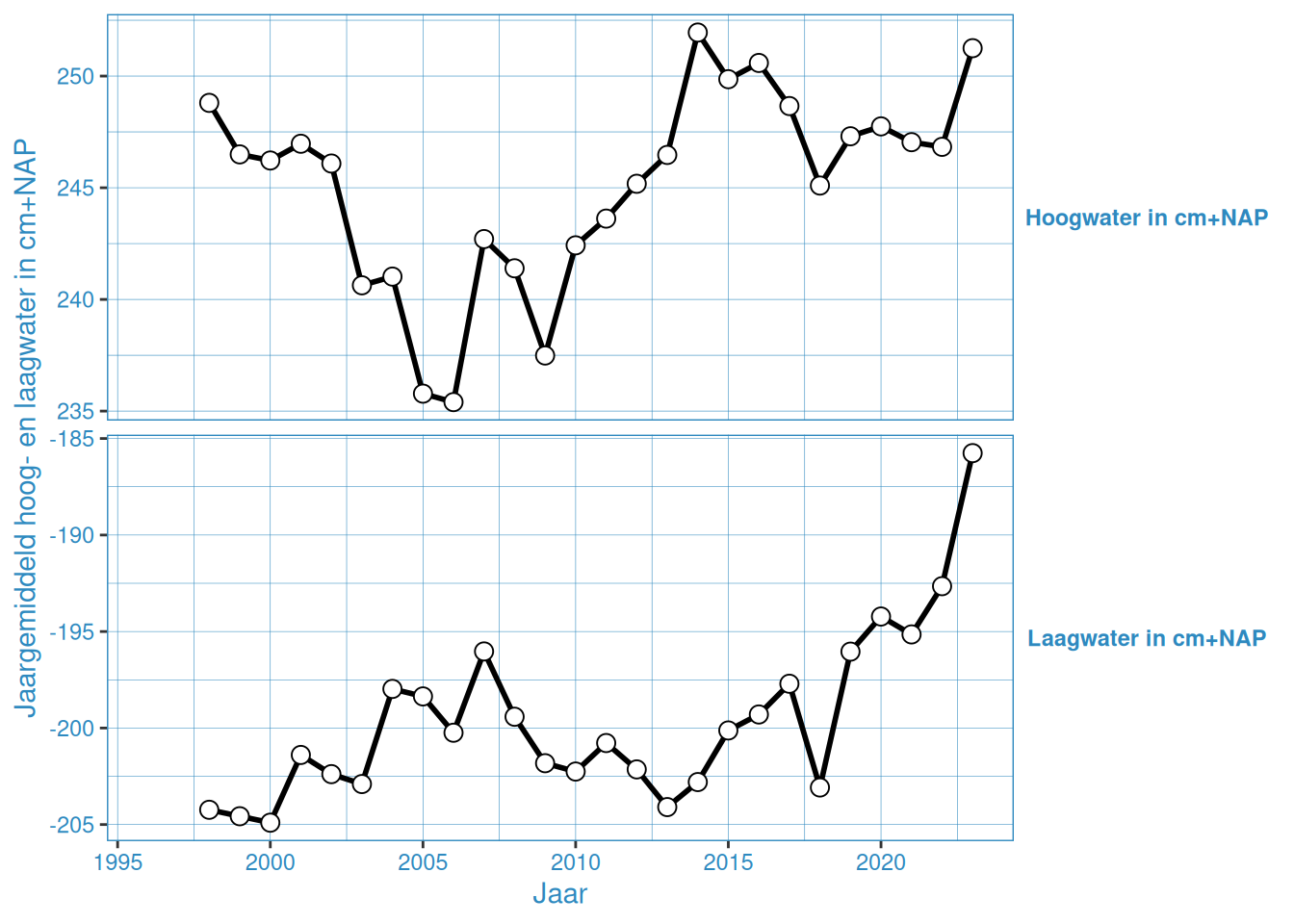
Figuur 2.12: Jaargemiddelde hoog- en laagwaterstanden bij Hansweert
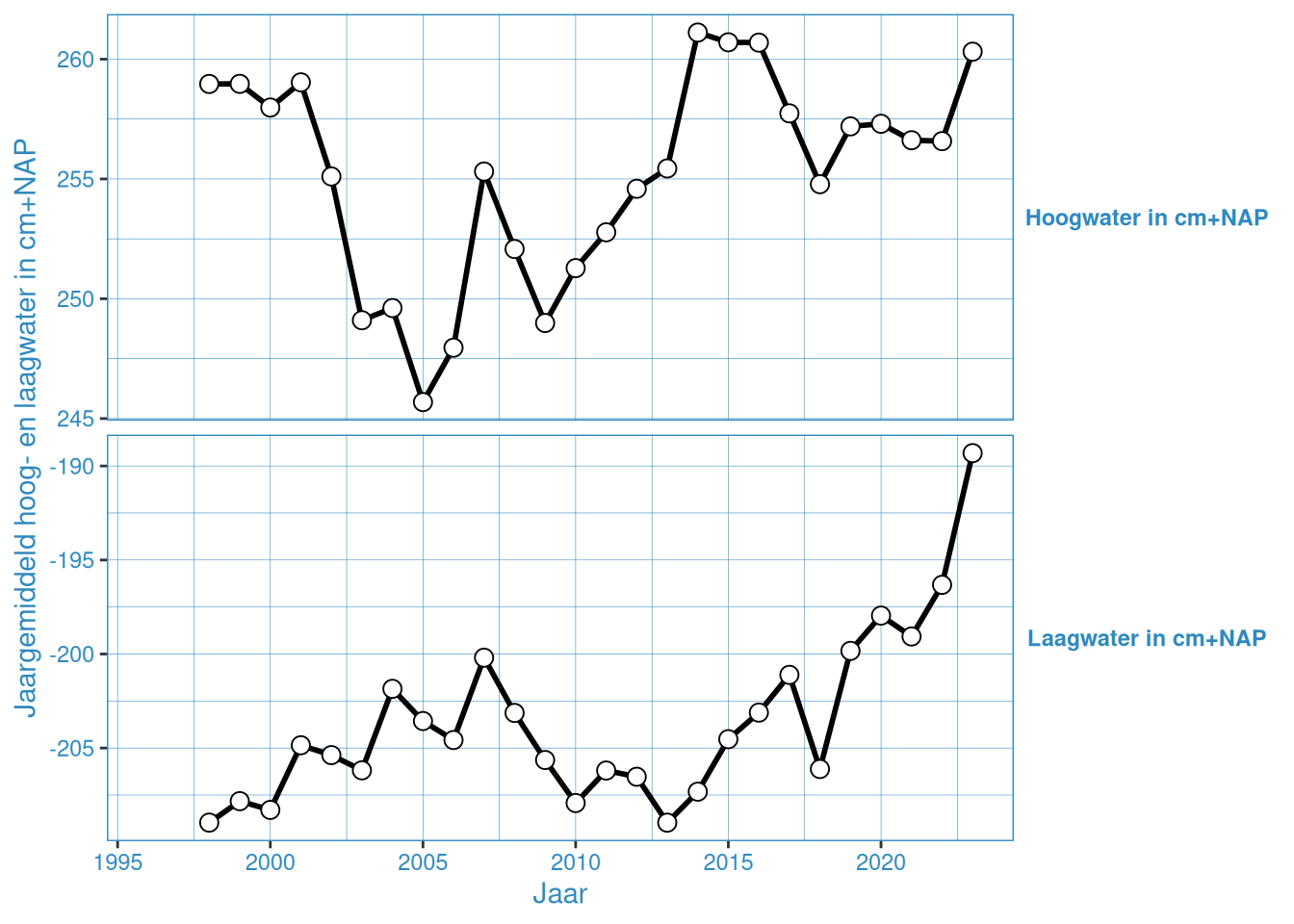
Figuur 2.13: Jaargemiddelde hoog- en laagwaterstanden bij Walsoorden
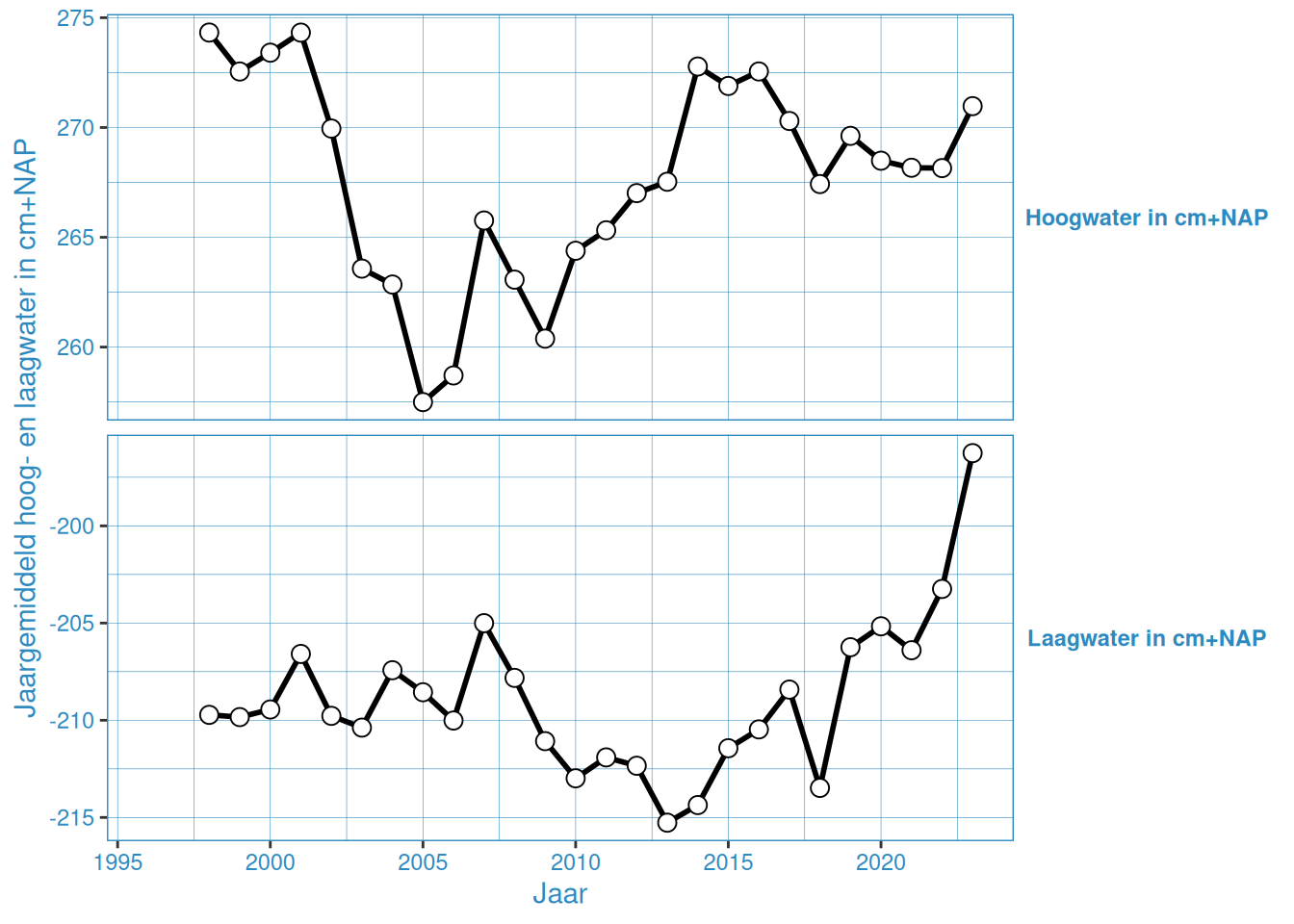
Figuur 2.14: Jaargemiddelde hoog- en laagwaterstanden bij Baalhoek
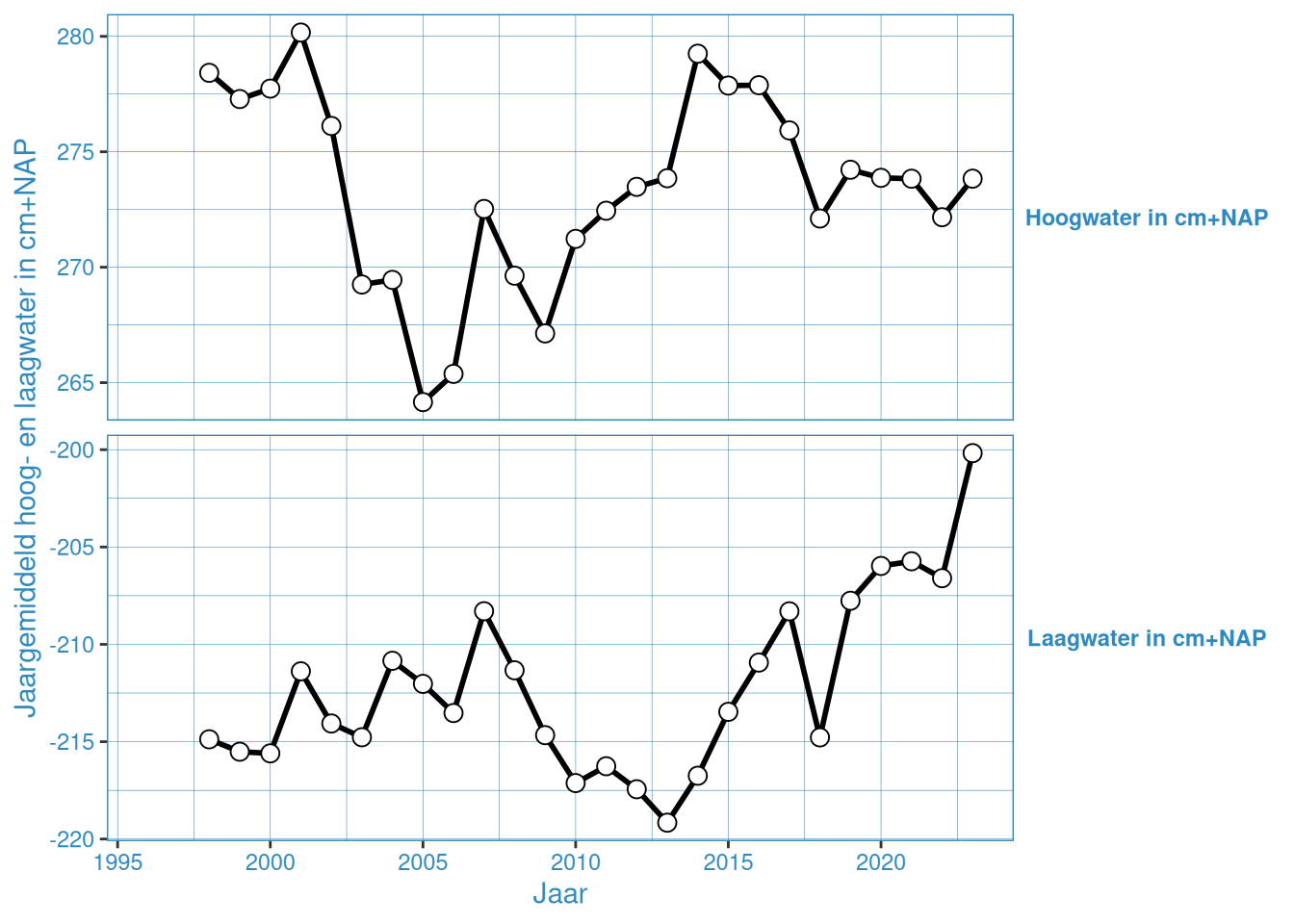
Figuur 2.15: Jaargemiddelde hoog- en laagwaterstanden bij Schaar van de Noord
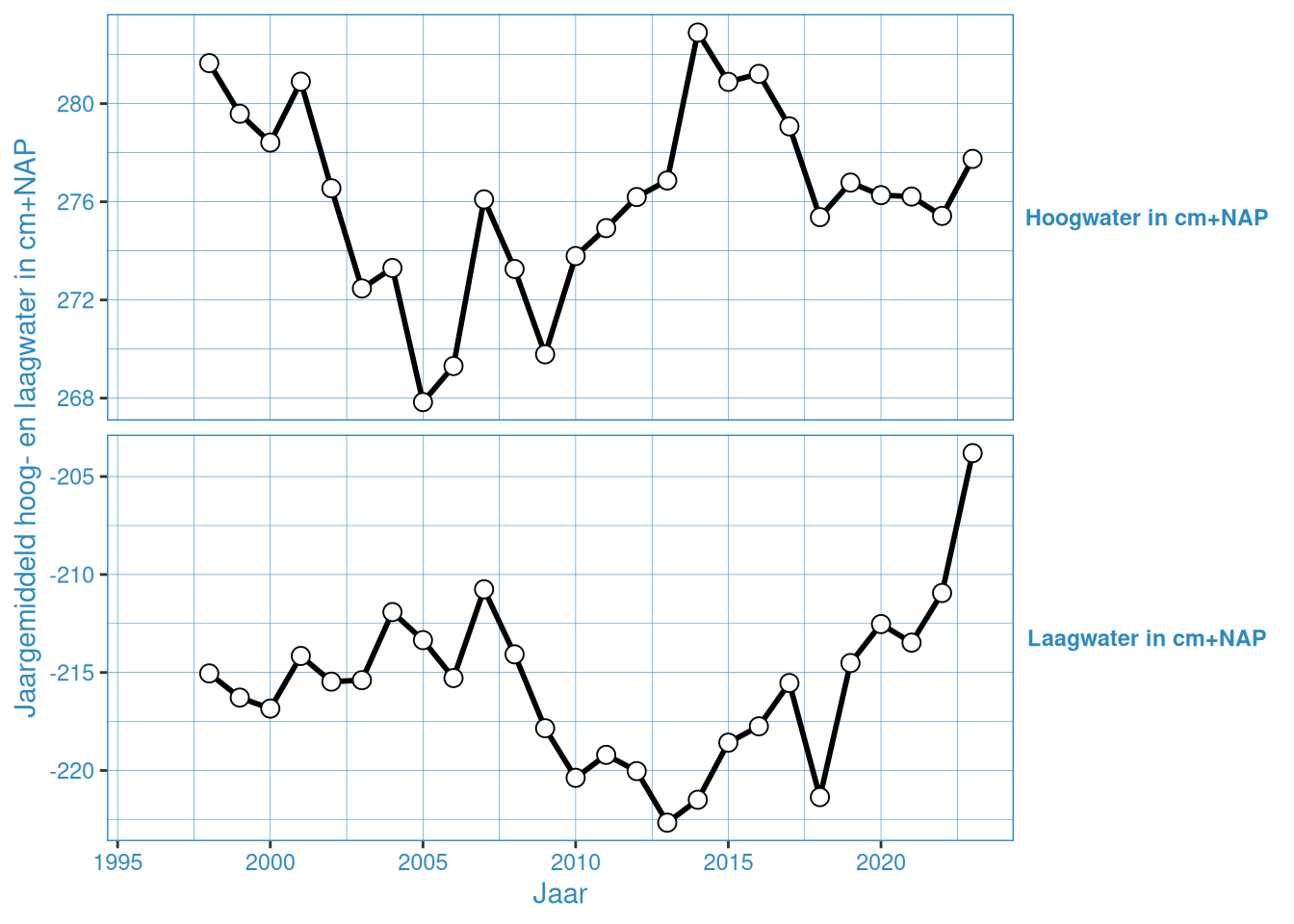
Figuur 2.16: Jaargemiddelde hoog- en laagwaterstanden bij Bath
Het Europlatform dient als referentiestation. Door de ligging in de Noordzee zijn de geregistreerde waterstanden bij dit station niet beïnvloed door vorm van het estuarium en de ligging in het estuarium. Bij het Europlatform bedraagt de gemiddelde hoogwaterstand tussen +0.9 en +1 m NAP. Laagwaterstanden bereiken gemiddeld een waarde van tussen de -0,75 en -0.65 m NAP.
De gemiddelde hoog- en laagwaterstand in Vlakte van de Raan is ongeveer gelijk gedurende de gehele meetperiode. De overige stations vertonenen een onderling vergelijkbaar patroon, waar er van grofweg 2005 tot 2015 een toename is van het gemiddeld hoogwater, en tussen 2005 en 2013 een afname van het gemiddeld laagwater. Na 2015 nemen de gemiddelde hoogwaters weer iets af, en na 2013 nemen de gemiddelde laagwaters weer iets toe.
Dit is waarschijnlijk de invloed van de 18,6-jarige cyclus, zoals ook duidelijk te zien is in de getijslag (Figuur 2.19). Bij de getijslag is dit effect duidelijker te zien, omdat dan de hoog- en laagwaterstand bij elkaar worden opgeteld waardoor het effect twee keer wordt meegeteld.
Vanaf de Vlakte van de Raan in oostwaartse richting zakt de gemiddelde laagwaterstand van circa -1,50 m NAP tot circa -1,80 m NAP bij Gat van Borssele. De hoogwaterstand neemt in die richting licht toe, van circa +1,75 m NAP bij de Vlakte van de Raan tot circa +2,25 m NAP bij Gat van Borssele. Hoewel Westkapelle en Cadzand ongeveer even ver in de monding liggen, is de getijslag bij Westkapelle minder groot dan bij Cadzand. Dit komt door de vervorming van het getij in de Noordzee, waardoor de getijslag in de Noordzee niet overal gelijk is.
Daarnaast constateren we een toename van gemiddeld hoogwater en een afname van gemiddeld laagwater naarmate men meer stroomopwaarts (i.e. oostelijke richting) van de Westerschelde komt, zoals te zien in Figuur 2.17 en Figuur 2.18.
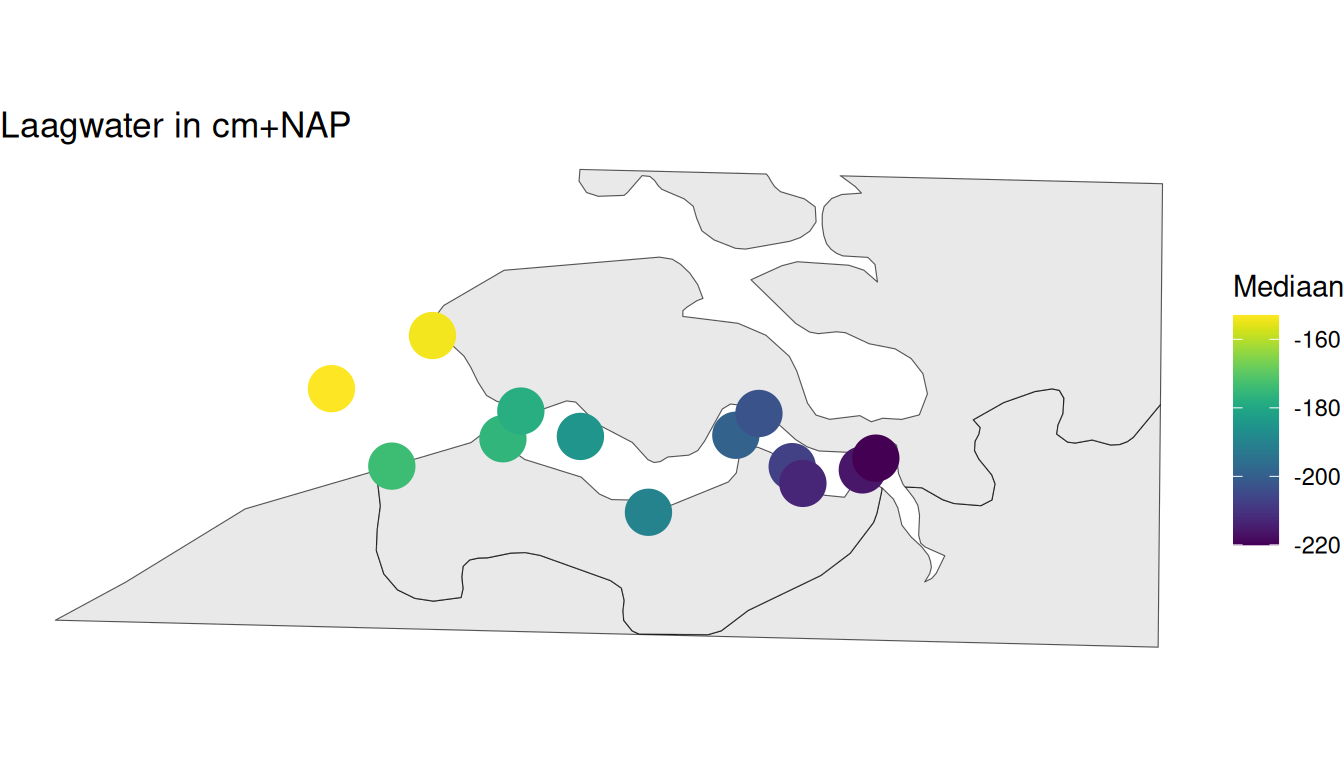
Figuur 2.17: Mediaan van laagwater per station berekend op alle beschikbare data vanaf 1998.
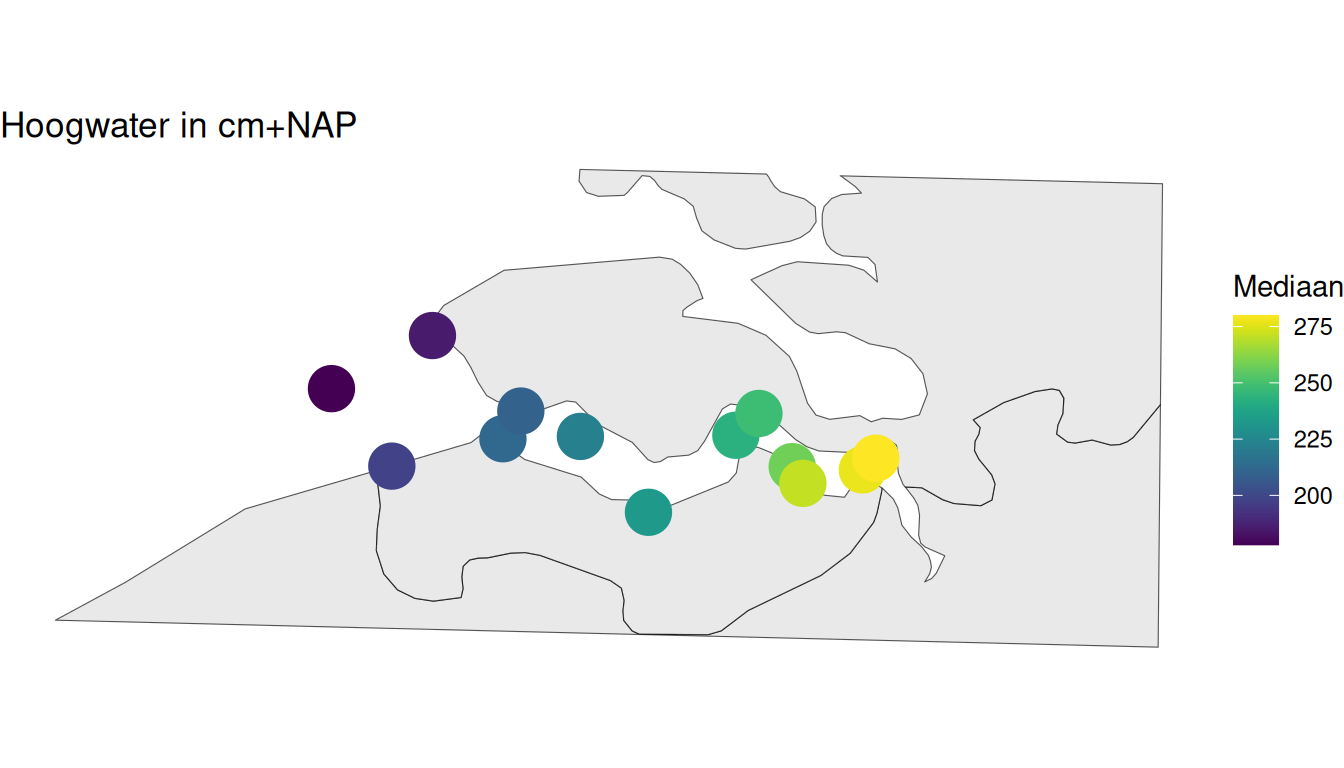
Figuur 2.18: Mediaan van hoogwater per station berekend op alle beschikbare data vanaf 1998
2.1.3 Jaargemiddelde getijslag
De getijslag is voor alle meetstations bepaald aan de hand van het verschil tussen de jaargemiddelde hoog- en laagwaterstanden. Op de Noordzee bij het Europlatform bedraagt de getijslag ongeveer 1,65 m en is weinig variatie in de getijslag te zien. In de monding is de getijslag al toegenomen tot 3 à 3,5 m. Verder stroomopwaarts de Westerschelde op blijft de getijslag toenemen tot aan Schaar van de Noord. Daar is de getijslag met een waarde van bijna 5 m het grootst, zie Figuur 2.19, Figuur 2.20 en Tabel 2.1.
| Station | Hoogwater in cm | Laagwater in cm | Getijslag |
|---|---|---|---|
| Europlatform | 95 | -70 | 165 |
| Vlakte van de Raan | 179 | -153 | 332 |
| Westkapelle | 185 | -154 | 339 |
| Cadzand | 198 | -175 | 373 |
| Vlissingen | 210 | -178 | 388 |
| Breskens Veerhaven | 212 | -177 | 389 |
| Gat van Borssele | 222 | -186 | 408 |
| Terneuzen | 233 | -190 | 423 |
| Overloop van Hansweert | 243 | -200 | 443 |
| Hansweert | 247 | -204 | 451 |
| Walsoorden | 258 | -208 | 466 |
| Baalhoek | 271 | -213 | 484 |
| Schaar van de Noord | 277 | -217 | 494 |
| Bath | 280 | -220 | 500 |
Figuur 2.19: De mediaan van getijslag over tijd op de Noordzee, in de monding en in de Westerschelde. Dunnere en transparante kleuren geven jaarlijkse gemiddeldes aan met twee of meer maanden met missende data.
De 18,6-jarige getijdencyclus heeft een grote invloed op de resultaten en is duidelijk zichtbaar in de figuren. De 18,6-jarige cyclus zorgt voor een periodieke toe- en afname van de waterstand en getijslag en is maximaal rond 1997 en 2014. Dit geldt voor stations zowel binnen als buiten de Westerschelde. Na 2014 is de getijslag weer toegenomen. De getijslag wordt groter stroomopwaarts. De versterking in de stroomopwaartse richting wordt voornamelijk veroorzaakt door de vorm van het estuarium (ondieper en smaller in stroomopwaartse richting).
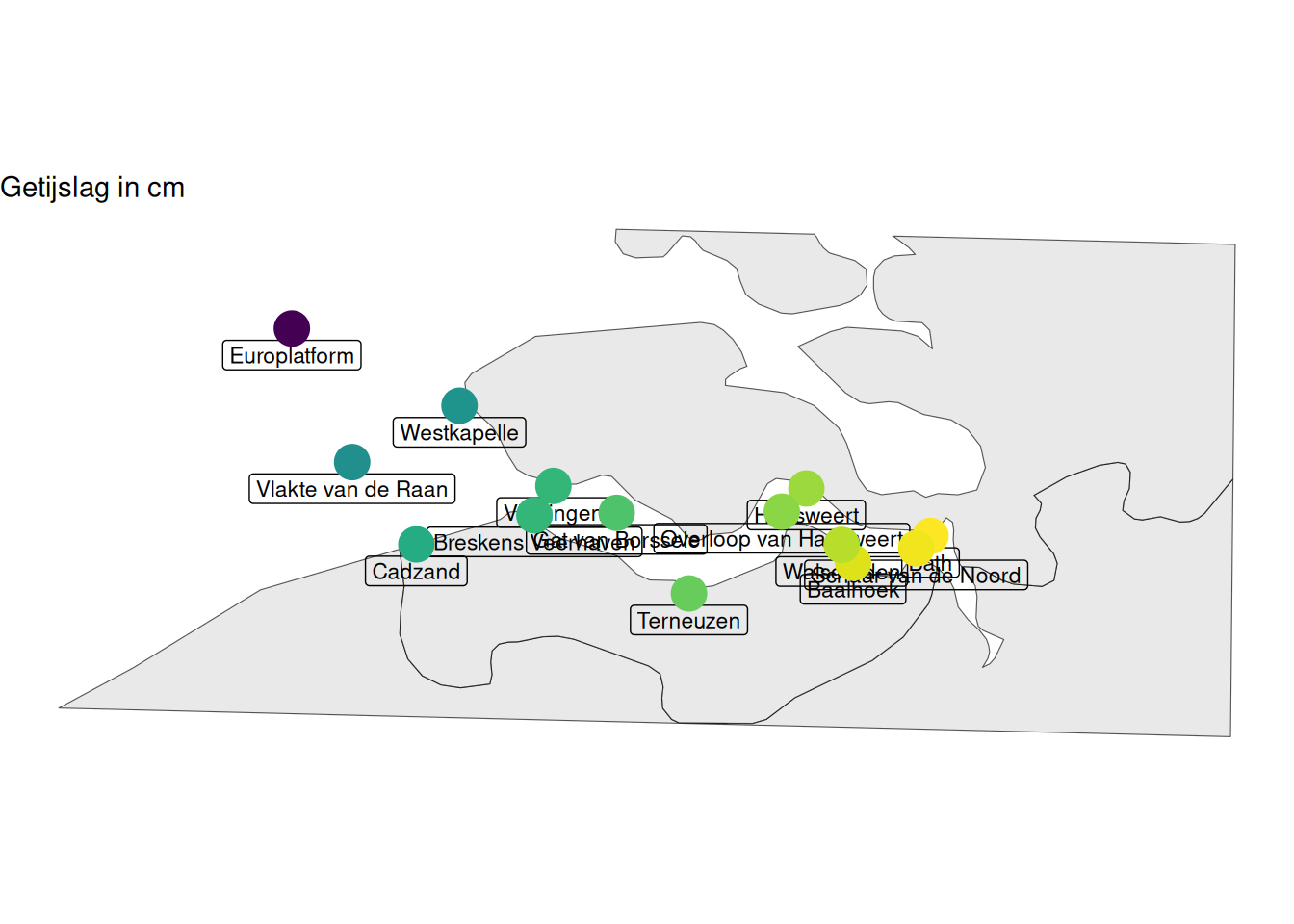
Figuur 2.20: Mediaan van getijslag per station berekend op alle beschikbare data vanaf 1998
In 2013 en 2014 werd de licht stijgende trend in de getijslag sinds 2007 doorgezet, conform de 18,6-jarige cyclus. Sinds 2015 neemt de getijslag juist weer licht af (figuur 2.19), wat strookt met het idee dat de 18,6-jarige cyclus de dominante oorzaak is van de trend in de getijslag. Dit wordt ook door de licht dalende trend in 2017 bevestigd. Dit lijkt niet op te gaan voor Breskens dat nog wel een stijgende lijn laat zien in 2016 ten opzichte van 2015, maar voor de periode na september 2016 zijn voor Breskens geen gegevens beschikbaar en kan de trend hierdoor niet worden bevestigd. In 2018 stijgt de getijslag ten opzichte van 2017 bij bijna alle stations. Terwijl in 2019 de getijslag t.o.v. 2018 weer daalt. Hierdoor lijkt de trend zich weer voort te zetten.
2.1.4 Getijcomponenten
Het gemeten waterstandssignaal kan geanalyseerd worden met een getijanalyse. Hierbij wordt het waterstandssignaal ontleed in verschillende harmonische componenten: sinussen met een zekere amplitude, frequentie en fase. De amplituden en fases van de M2, M4 en S2 componenten worden weergegeven in Figuur 2.21 tot en met 2.26 en in Tabel 2.2.
| Station | M2.ampl | M4.ampl | S2.ampl | M2.fase | M4.fase | S2.fase |
|---|---|---|---|---|---|---|
| Europlatform | 74 | 10 | 18 | 53 | 130 | 110 |
| Cadzand | 170 | 12 | 47 | 49 | 90 | 110 |
| Westkapelle | 150 | 14 | 42 | 53 | 96 | 110 |
| Vlissingen | 170 | 13 | 48 | 59 | 120 | 120 |
| Terneuzen | 190 | 12 | 50 | 69 | 130 | 130 |
| Hansweert | 200 | 11 | 52 | 80 | 160 | 140 |
| Schaar van de Noord | 210 | 12 | 54 | 89 | 180 | 150 |
| Bath | 210 | 11 | 55 | 91 | 180 | 150 |
De amplitude van de M2-component neemt toe in stroomopwaartse richting: de trechtervorm van het estuarium veroorzaakt een opslingering van het getij. In de tijd zien we in de oostelijkere stations, en vooral bij Bath, een toename van de amplitude. Dit komt overeen met het beeld uit de hoog- en laagwaterstanden. Tussen ongeveer 2014 en 2018 vertoont de amplitude van de M2-component een licht dalende trend (met name voor de meer oostelijke stations) met wat kleinere schommelingen. De dalende trend is daarna afgevlakt.
De fase van de M2-component hangt af van de positie in het estuarium, door de looptijd van het getij daar doorheen. De M2 fase is in de loop van de jaren 1998-2022 niet veel veranderd.
De amplitude van de M4-component laat een tegenovergestelde ruimtelijke relatie als de M2-component zien. Hiermee wordt bedoeld dat de M4 afneemt voor oostelijkere stations. De S2-component gedraagt zich vergelijkbaar met de M2-component. De amplitude van de S2- en M4-componenten varieert slechts beperkt over de tijd, behalve bij Bath, waar een sterke afname is te zien over de getoonde periode voor de M4 amplitude.
Over de getoonde periode (1998-2022) neemt de fase van de M4-component bij Hansweert en bij Bath iets af. Voor de overige stations is de fase gelijk over dze periode.
Figuur 2.21: Amplitude van de M2-getijcomponent voor de landelijke meetstations.
Figuur 2.22: Amplitude van de M4-getijcomponent voor de landelijke meetstations.
Figuur 2.23: Amplitude van de S2-getijcomponent voor de landelijke meetstations.
Figuur 2.24: Fase van de M2-getijcomponent voor de landelijke meetstations.
Figuur 2.25: Fase van de M4-getijcomponent voor de landelijke meetstations.
Figuur 2.26: Fase van de S2-getijcomponent voor de landelijke meetstations.
2.2 Golven
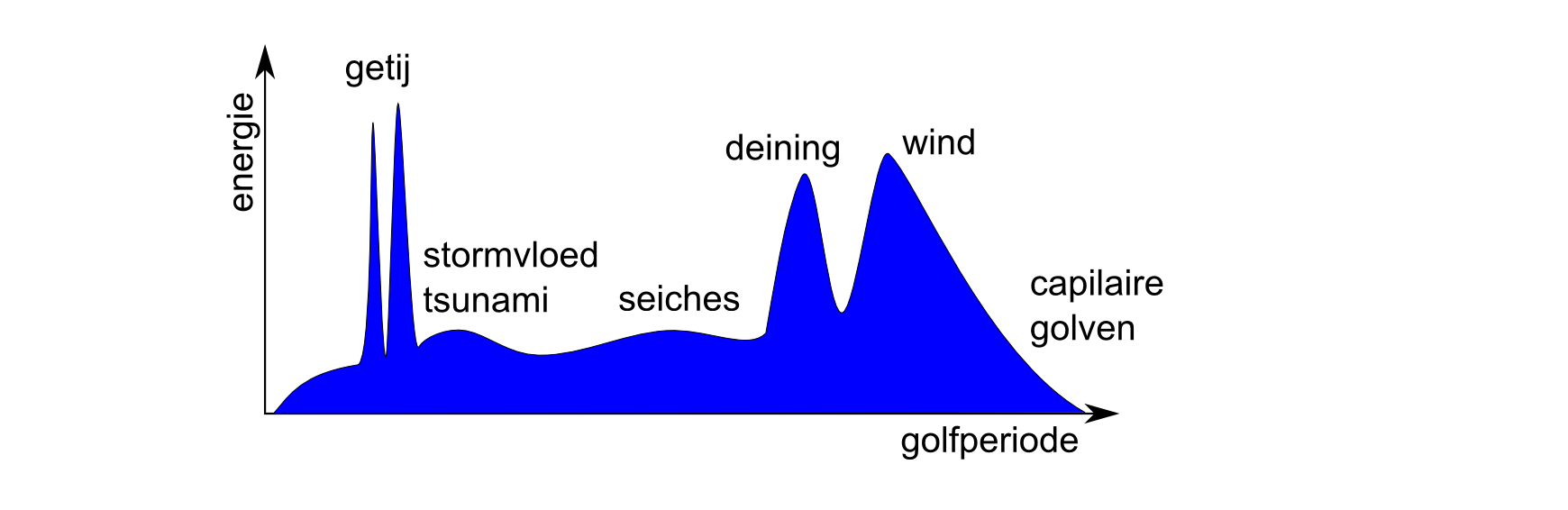
Figuur 2.27: Voorbeeld van een geschematiseerd golfspectrum op zee (naar: www.infrawiki.nl).
Golven die voorkomen op de Noordzee en in de Westerschelde hebben steeds verschillende golfhoogte, -periode en richting. Dit is afhankelijk van de wind (kracht, duur, richting, strijklengte), de waterdiepte en de golfvoortplanting. Van golfmetingen wordt meestal per 15 minuten een spectrum afgeleid, waarin golven met verschillende golfhoogte en -periode (in de vorm van een frequentie = 1 / periode) zijn opgenomen, zie Figuur 2.27. De golven die in deze paragraaf worden meegenomen bevinden zich aan de rechterkant van het in Figuur 2.27 weergegeven spectrum en zijn aangeduid met deining en wind. Deining wordt veroorzaakt door golfvoortplanting van golven die verder weg zijn opgewekt. Windgolven zijn lokaal opgewekte golven.
Een belangrijke golfkarakteristiek is de significante golfhoogte. De significante golfhoogte kan op twee verschillende manieren berekend worden: als het gemiddelde van het hoogste 1/3 deel van de golven in een tijdsbestek van 10 minuten (\(H_{1/3}\)) of uit het energiedichtheidsspectrum (\(H_{m0}\)) op basis van viermaal de standaardafwijking. Hoewel beide methodes een andere berekeningswijze hebben (de eerste gaat uit van de hoogte van individuele golven, de tweede wordt berekend uit het energiedichtheidsspectrum), komt het resultaat in hoge mate overeen. De significante golfhoogte komt goed overeen met de op het oog geschatte golfhoogte (Holthuijsen (2007)). Vroeger werden golven op die manier gemeten (o.a. vanaf schepen), waardoor het een belangrijke parameter is geworden in de golfstatistiek.
In deze rapportage wordt steeds het maandelijkse gemiddelde en het maandelijkse maximum van de significante golfhoogte weergegeven. Het maximum van de significante golfhoogte per maand betreft dus geen maximum van alle individuele golven in die maand, maar het maximum van het gemiddelde 1/3 hoogste deel in een periode van 10 minuten of het maximum van de significante golfhoogte uit het spectrum.
Naast de golfhoogte wordt ook de golfperiode gerapporteerd, zowel de gemiddelde periode van het hoogste 1/3 deel van de golven (\(T_{H,1/3}\)), als de gemiddelde golfperiode van alle golven berekend uit het spectrum (\(T_{m02}\)). \(T_{m02}\) wordt bepaald uit het spectrale gemiddelde van het kwadraat van de frequentie en is daarom in het algemeen lager dan \(T_{H,1/3}\). \(T_{m02}\) is dus niet direct gerelateerd aan \(H_{m0}\).
Op verzoek van RWS worden de golfrozen sinds de Eerstelijnsrapportage 2015 niet meer weergegeven. Dit heeft te maken met kleine wijzigingen in rekenparameters in de Evaluatiesystematiek (update 2014). Echter zijn golfrichting metingen van belang voor bijvoorbeeld aanvallen op de kust. Daarom is het verstandig om in de volgende rapportage deze metingen weer op te nemen.
2.2.1 Informatie over de metingen
Golven worden in de Westerschelde en in de monding op een aantal stations (zie Figuur 2.28) gemeten. Niet op alle stations wordt met dezelfde instrumenten gemeten. Ook in de tijd heeft er een verschuiving plaatsgevonden in het frequentiebereik van de metingen. Het frequentiebereik wordt van tevoren ingesteld aan de hand van de te verwachten golfperioden op de betreffende locatie. Het frequentiebereik is aangeduid als:
- GSO2 met een frequentiebereik van 0 tot 700 mHz
- GHr2 met een frequentiebereik van 0 tot 1000 mHz
- GDr2 met een frequentiebereik van 0 tot 500 mHz
De parameters die uit het spectrum worden bepaald, de significante golfhoogte \(H_{m0}\) en periodeparameter \(T_{m02}\), zijn berekend uit het deel van het spectrum van 30 mHz tot de bovengrens (700, 1000 en 500 mHz). Voor GSO2 is geen significante golfhoogte uit het spectrum bepaald. In Tabel 2.3 zijn de verschillende aanduidingen en meetinstrumenten per station en per meetperiode gegeven. Gemiddelde, minimale en maximale waardes in bijgevoegde tabellen zijn gebaseerd over de tijdsperiode weergegeven in de figuren. In Tabel 2.3 is te zien dat voor Hoofdplaat sinds januari 2016 geen nieuwe data beschikbaar is.
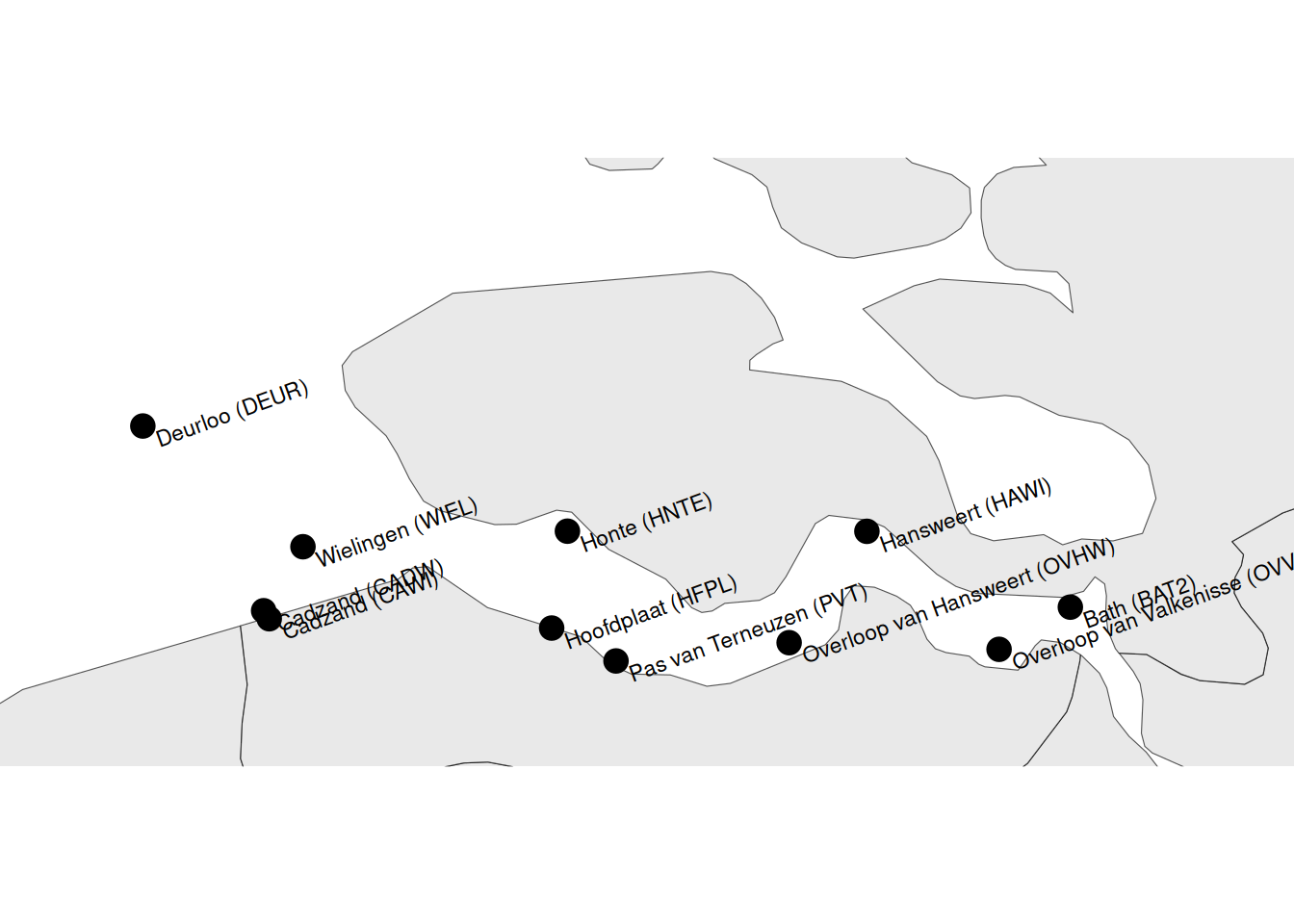
Figuur 2.28: Ligging van de meetstations voor de golfhoogte en -periode.
| Meetstation | Code | Meetinstrument |
|---|---|---|
| Bath | BAT2 | Golfbraak |
| Cadzand | CADW | Directional waverider |
| Deurloo | DEUR | Directional waverider |
| Hansweert | HAWI | Golfbraak |
| Honte | HNTE | Boei |
| Hoofdplaat | HFPL | Golfbraak |
| Overloop van Hansweert | OVHW | Golfbraak |
| Overloop van Valkenisse | OVVA | Golfbraak |
| Pas van Terneuzen | PVT | Waverider |
| Wielingen | WIEL | Waverider |
Voor de metingen van golven worden verschillende meetinstrumenten gebruikt. Hieronder een uitleg over de instrumenten:
Directional waverider De directional waverider is een boei die de verticale versnellingen en horizontale plaatsen, ‘pitch’, ‘roll’ en ‘heave’ meet. Bovendien is de boei uitgerust met twee vaste versnellingsmeters, een kompas en een richtingsmeter. Het golffrequentiebereik van de directional waverider wordt verschillend ingesteld afhankelijk van de ligging van de boei en de daarvoor te verwachte golfperioden. Op de Noordzee en de Delta is het golffrequentiebereik van directional waverider ingesteld op 0,03 Hz – 0,5 Hz (GDr2). Omdat in de Westerschelde de golven over het algemeen korter zijn (kleinere periode dus een grotere frequentie) is het golffrequentiebereik hoger ingesteld namelijk: 0,03 Hz – 1,0 Hz (GHr2). De bemonsteringsfrequentie van de directional waverider is 1,28 Hz.
Waverider De waverider is een bolvormige boei. Deze boei meet de versnellingen in verticale richting, die worden veroorzaakt door de golfkrachten op de boei. Hieruit kunnen de hoogteveranderingen van het zeeoppervlak worden berekend en daaruit kunnen weer golfkarakteristieken worden bepaald. Het golffrequentiebereik van de waverider wordt verschillend ingesteld afhankelijk van de ligging van de boei en de daarvoor te verwachte golfperioden. Op de Noordzee en de Delta is het golffrequentiebereik van waverider ingesteld op 0,03 Hz – 0,5 Hz (GDr2). Omdat in de Westerschelde de golven over het algemeen korter zijn (kleinere periode dus een grotere frequentie) is het golffrequentiebereik hoger ingesteld namelijk: 0,03 Hz – 1,0 Hz (GHr2). De bemonsteringsfrequentie is 2,56 Hz.
Golfbraak Een golfbraak is een verticaal gemonteerde kunststofbuis, waaraan op regelmatige afstanden van 5 cm elektroden zijn bevestigd aan de hand waarvan continue wordt gemeten wat de hoogste elektrode is die zich nog onder water bevindt. Daarmee worden de veranderingen van het zeeoppervlak in de tijd vastgelegd en daaruit worden karakteristieken van de golfbeweging bepaald. De golfbraak is gemonteerd aan een platform of een meetpaal. De bemonsteringsfrequentie is 2,56 Hz.
2.2.2 Golfhoogte
De maandelijkse gemiddelden en maandelijkse maxima van de significante golfhoogte zijn weergegeven in Figuur 2.31 t/m Figuur 2.40 voor \(H_{1/3}\) (telkens bovenste figuur) en \(H_{m0}\) (telkens onderste figuur). De meetstations zijn gerangschikt in stroomopwaartse richting. Voor maanden met een kwart of meer aan missende data worden de gemiddeldes met dunnere en transparante kleuren weergegeven. Aan deze gemiddeldes kan minder waarde gehecht worden.
De significante golfhoogte, \(H_{1/3}\), komt voor windgolven goed overeen met de significante golfhoogte die bepaald is uit het spectrum, \(H_{m0}\). Op basis van de tijdseries per station constateren we geen trend in toe of afname van de golfhoogtes.
Zoals te verwachten zijn de golven in de monding (Deurloo, Cadzand, Wielingen) het hoogste, met gemiddelden van ~0.6 t/m 0.9 m en maxima net boven de 1.6 m bij Deurloo, zie ook Figuur 2.29. Niet al deze golven propageren de Westerschelde in. Alleen de golven die naar het (zuid)oosten bewegen propageren de Westerschelde in. Een deel van de golfenergie die wel richting de Westerschelde propageert, wordt verder gedissipeerd op de ondiepe delen in de monding en de Westerschelde. In de Westerschelde zijn de gemiddelde significante golfhoogtes daardoor een stuk lager, rond 20 cm, met maxima verschillend van 0.2 t/m 0.6 m. De meeste golven in de Westerschelde zijn lokaal opgewekte golven (door de wind, maar deels ook door schepen), waarbij de noordelijke boeien (Honte, Hansweert en Bath) een grotere golfhoogte laten zien dan de zuidelijke (Hoofdplaat en Pas van Terneuzen). Dit heeft waarschijnlijk te maken met een overheersende zuidwestenwind, waardoor de strijklengte van de noordelijke stations groter is.
Maximale significante golfhoogtes voor windgolven worden in de Westerschelde geschat op 1.5 meter op basis van Breugem and Holthuijsen (2006). Dit is gebaseerd op een strijklengte van 10 kilometer met een wind snelheid van 22 m/s. Golfhoogtes groter dan 1.5 meter zijn daarom te wijten aan schepen en/of meetfouten. Maximale golfhoogtes op de Noordzee zijn in de orde grootte van meerdere meters (e.g. \(H_s\) > 5 meter tijdens een grotere storm). Figuur 2.30 laat de empirische distributie van golfhoogte op basis van alle beschikbare data zien. Hierin constateren we dat de mediaan van de significante golfhoogte in de Westerschelde tussen de 10 en 75 centimeter ligt. Voor stations verder vanaf de monding is minder dan 10% groter dan 25 centimeter, terwijl in Deurloo dit 4x zo hoog is (i.e. 100 centimeter). Al met al lijkt de golfhoogte in de Westerschelde veelal lager dan 25 cm, terwijl de golfhoogte in de monding (i.e. Cadzand, Deurloo en Wielingen) tussen de 50 en 75 cm ligt. Voor sommige locaties treedt wel eens een groot verschil tussen \(H_{1/3}\) en \(H_{m0}\) op. Dit wijst erop dat het scheepsgolven of meetfouten betreft en geen windgolven.
| Station | Hm0 med | Hm0 max | H1/3 med | H1/3 max |
|---|---|---|---|---|
| Bath (BAT2) | 20 | 43 | 20 | 42 |
| Hansweert (HAWI) | 23 | 52 | 23 | 50 |
| Cadzand (CAWI) | 56 | 100 | 55 | 100 |
| Cadzand (CADW) | 56 | 150 | 52 | 130 |
| Overloop van Hansweert (OVHW) | 20 | 40 | 19 | 38 |
| Deurloo (DEUR) | 92 | 150 | 82 | 190 |
| Honte (HNTE) | 26 | 59 | 26 | 57 |
| Hoofdplaat (HFPL) | 12 | 20 | 11 | 19 |
| Overloop van Valkenisse (OVVA) | 15 | 26 | 15 | 25 |
| Pas van Terneuzen (PVT) | 18 | 25 | 18 | 24 |
| Wielingen (WIEL) | 58 | 110 | 55 | 110 |
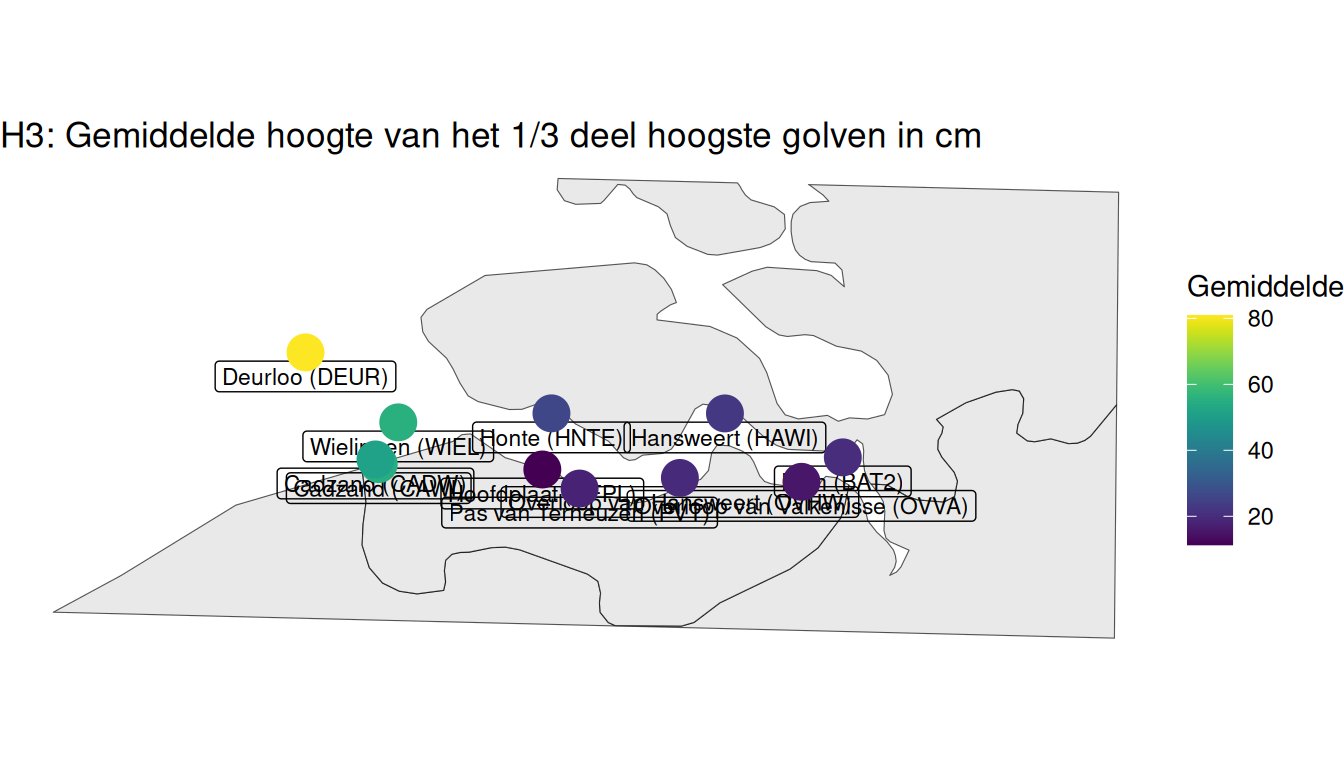
Figuur 2.29: Gewogen gemiddelde significante golfhoogte per station berekend op basis van het spectrum voor alle beschikbare data vanaf 1998.
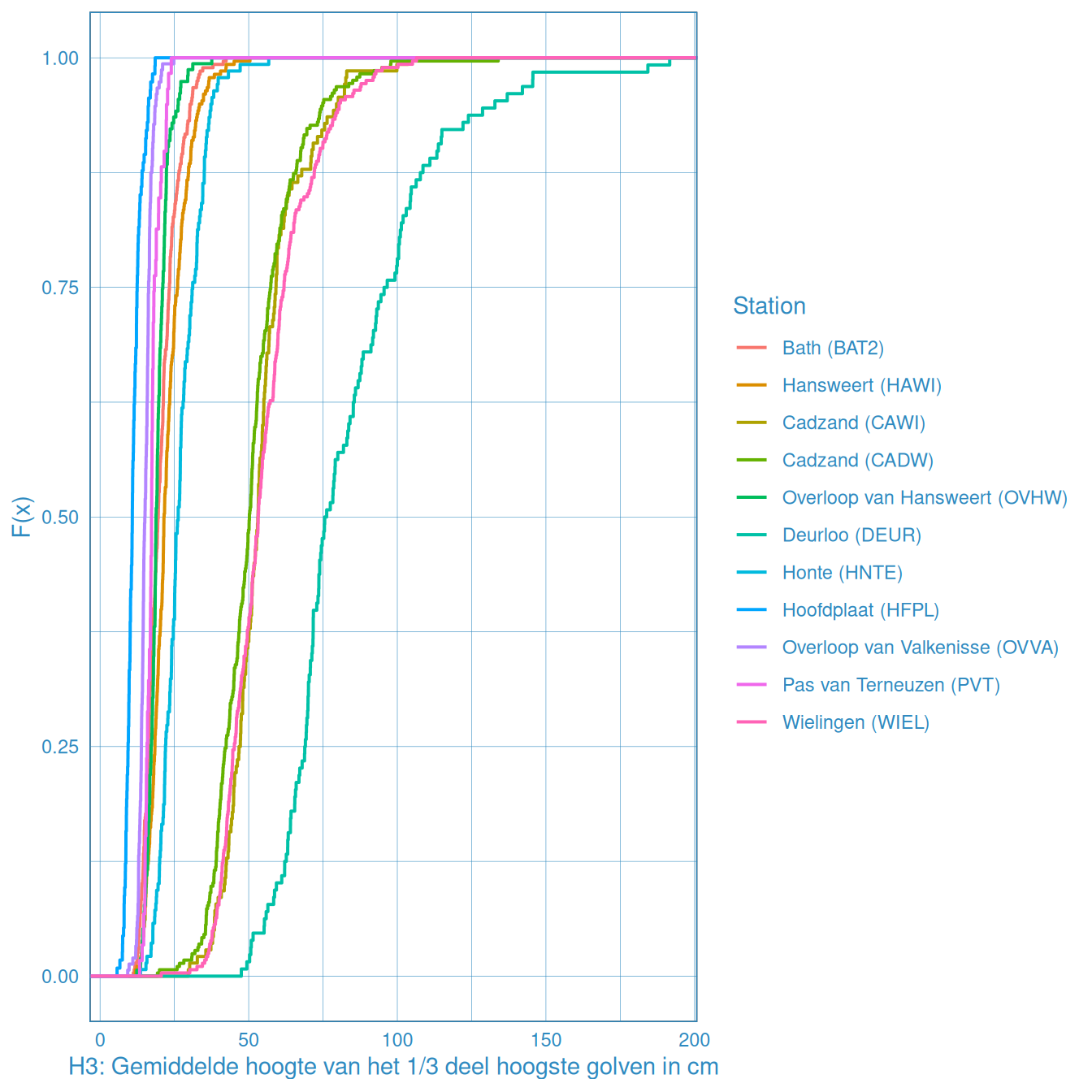
Figuur 2.30: Empirische distributiefunctie voor de significante golfhoogte berekend op basis van het spectrum voor alle beschikbare data vanaf 1998.
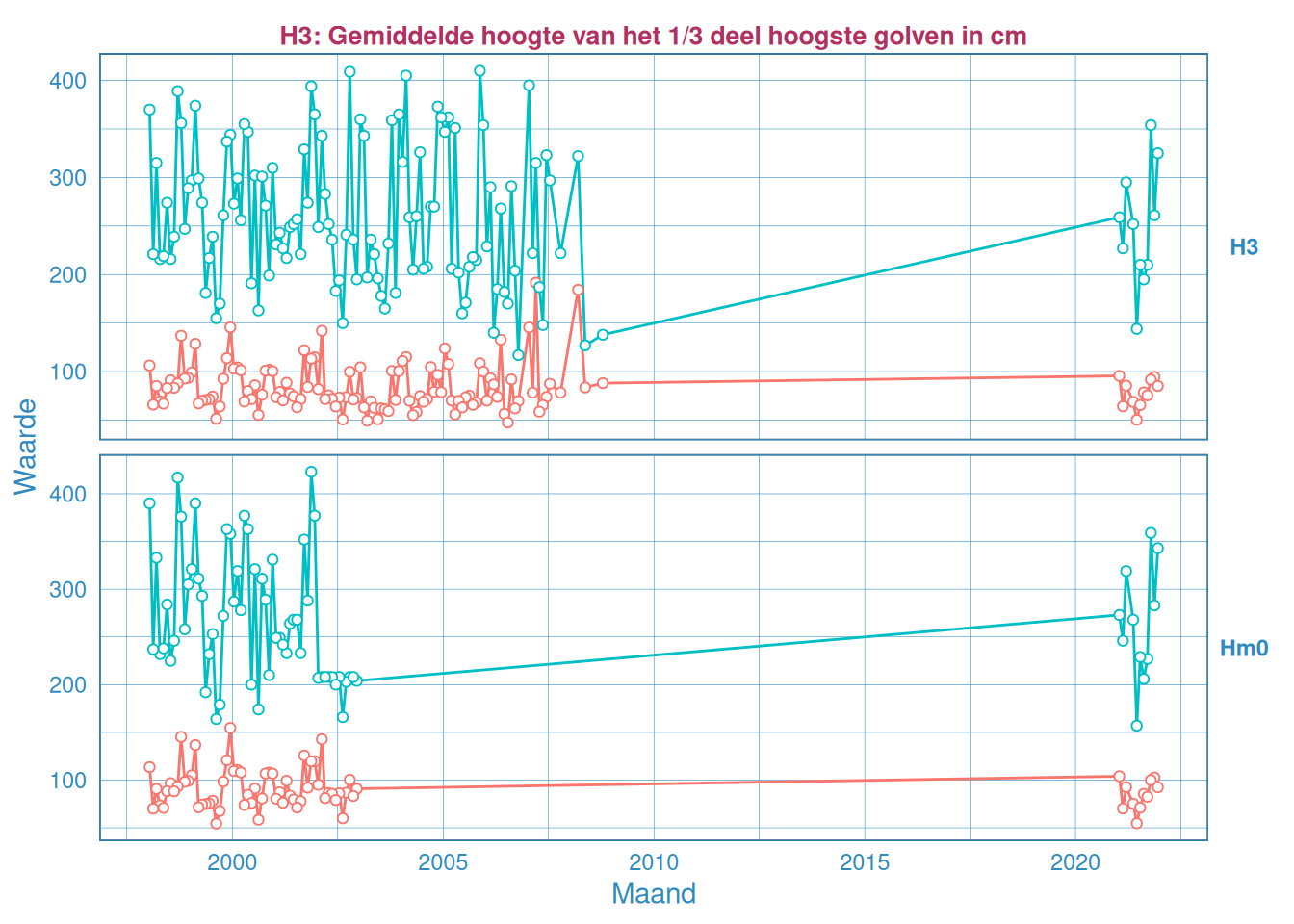
Figuur 2.31: Maandelijks gemiddelde en maximum van de significante golfhoogte \(H_{1/3}\) (boven) en \(H_{m0}\) (onder) voor station Deurloo.
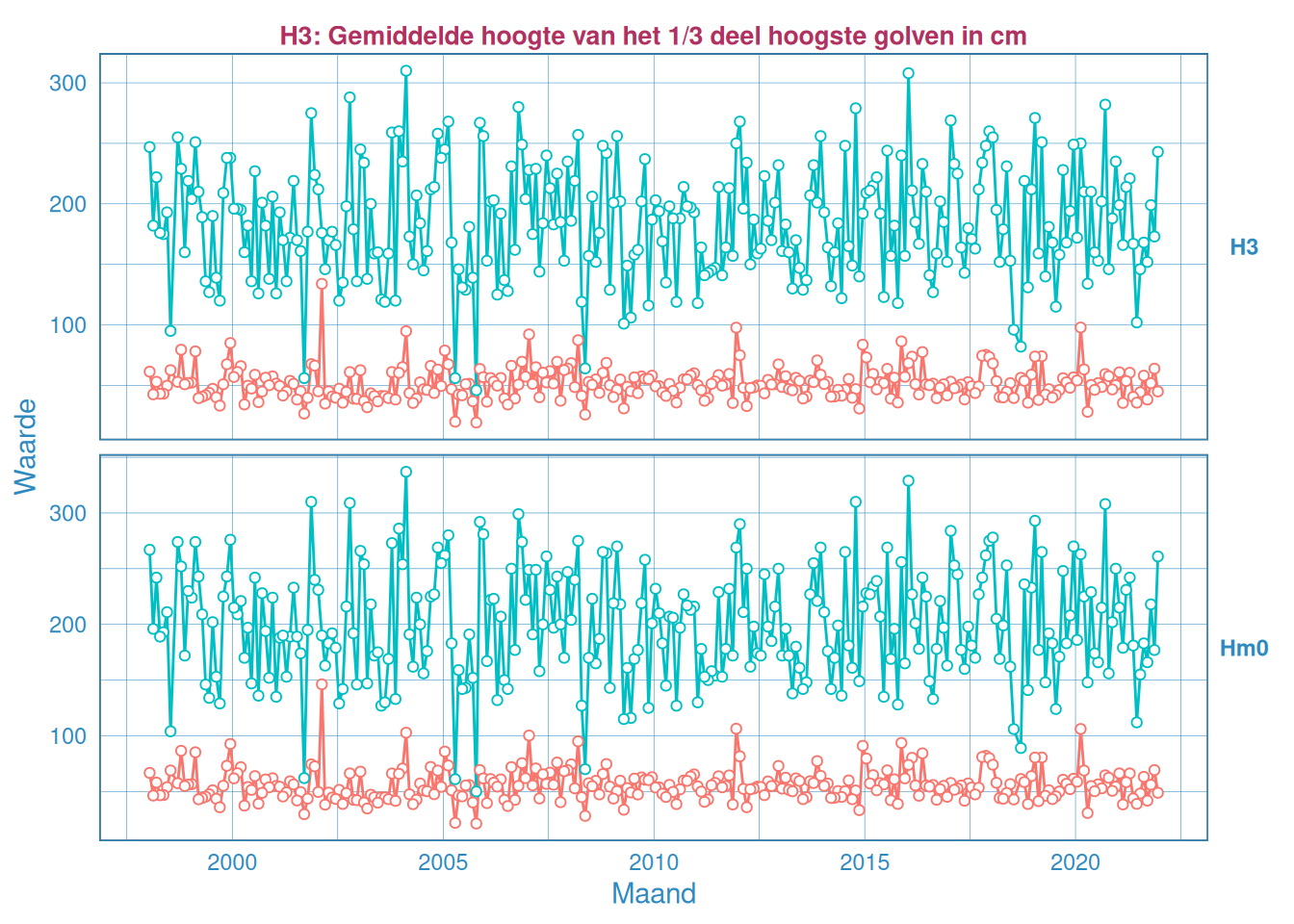
Figuur 2.32: Maandelijks gemiddelde en maximum van de significante golfhoogte \(H_{1/3}\) (boven) en \(H_{m0}\) (onder) voor station Cadzand
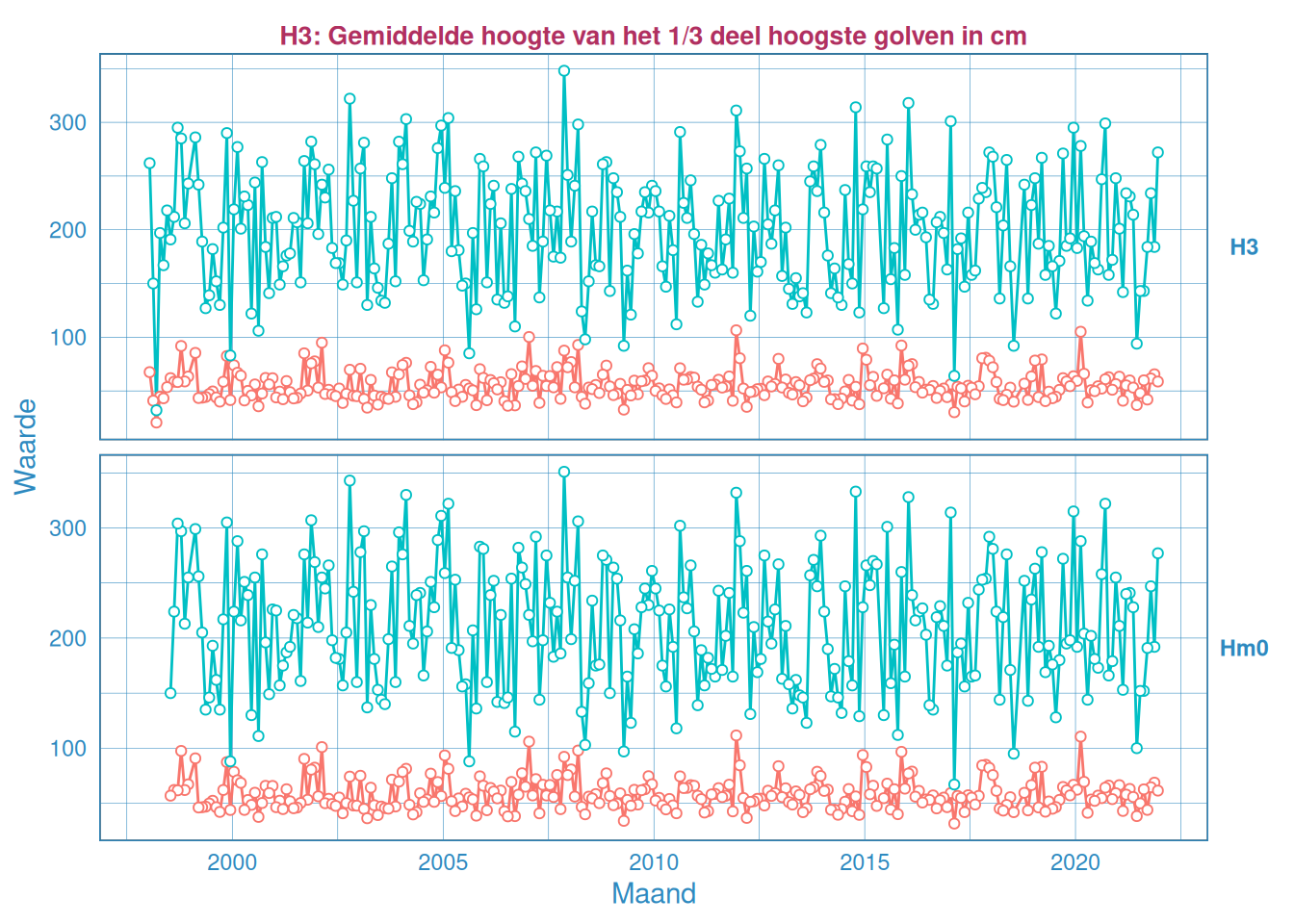
Figuur 2.33: Maandelijks gemiddelde en maximum van de significante golfhoogte \(H_{1/3}\) (boven) en \(H_{m0}\) (onder) voor station Wielingen
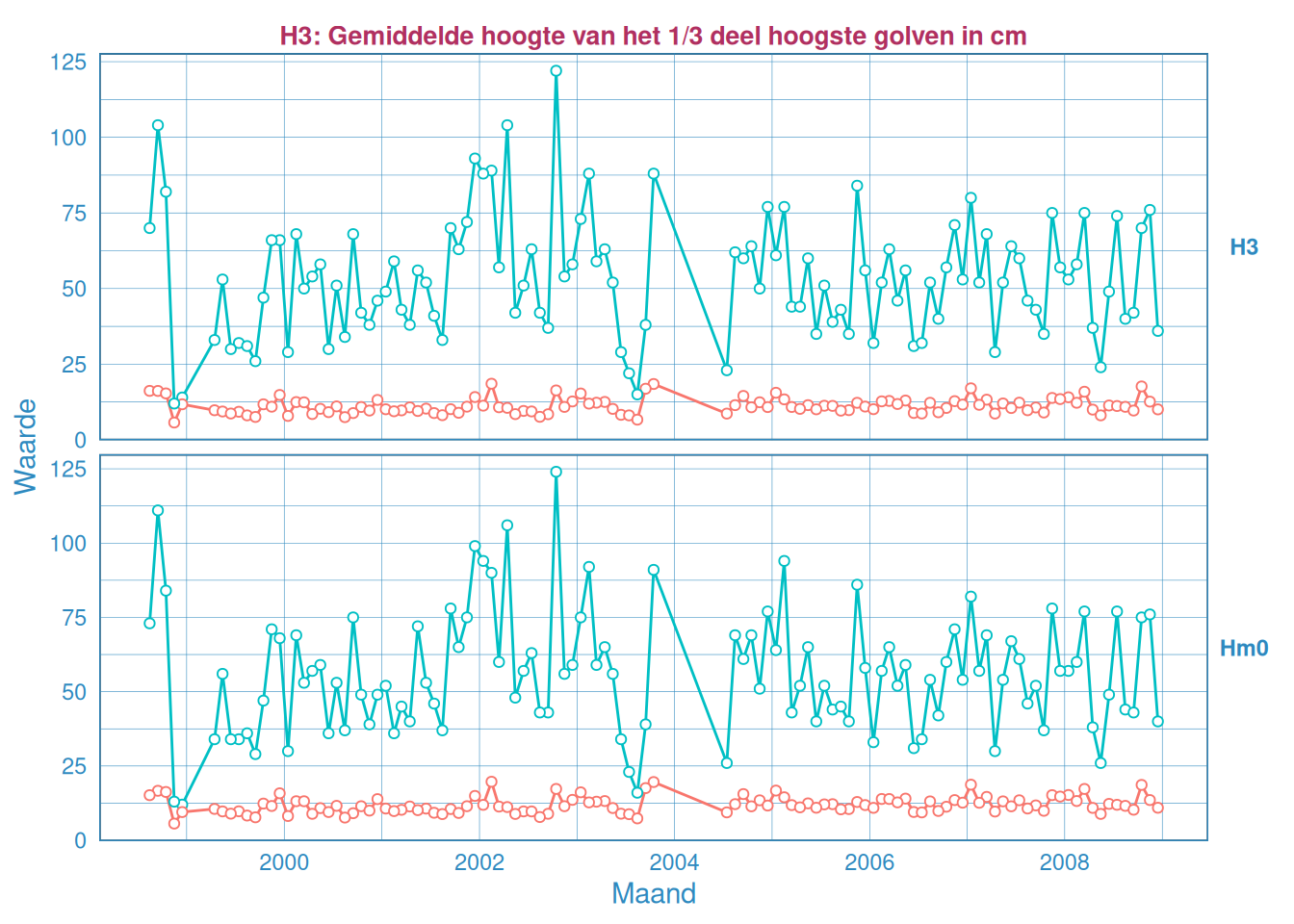
Figuur 2.34: Maandelijks gemiddelde en maximum van de significante golfhoogte \(H_{1/3}\) (boven) en \(H_{m0}\) (onder) voor station Hoofdplaat.
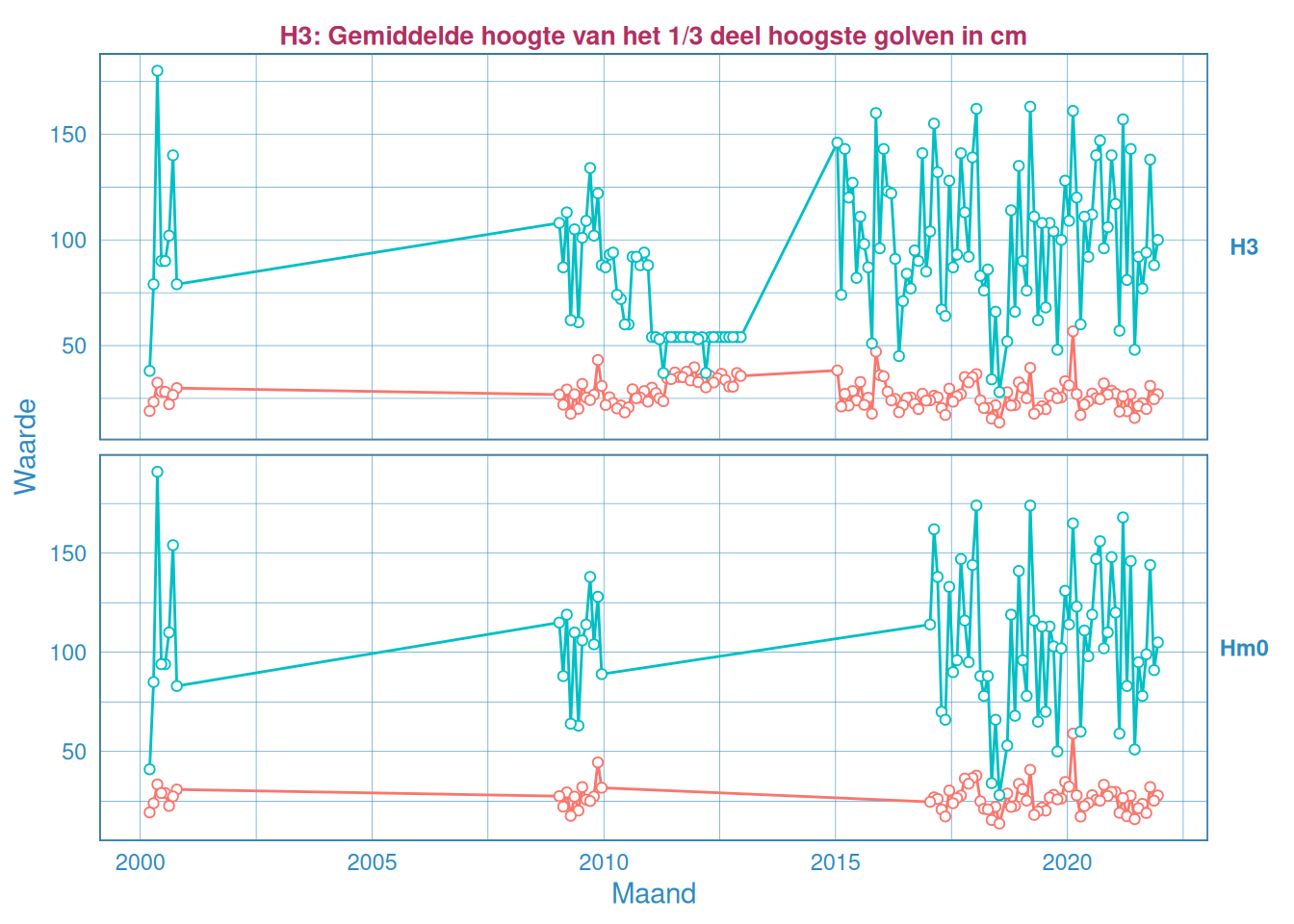
Figuur 2.35: Maandelijks gemiddelde en maximum van de significante golfhoogte \(H_{1/3}\) (boven) en \(H_{m0}\) (onder) voor station Honte.
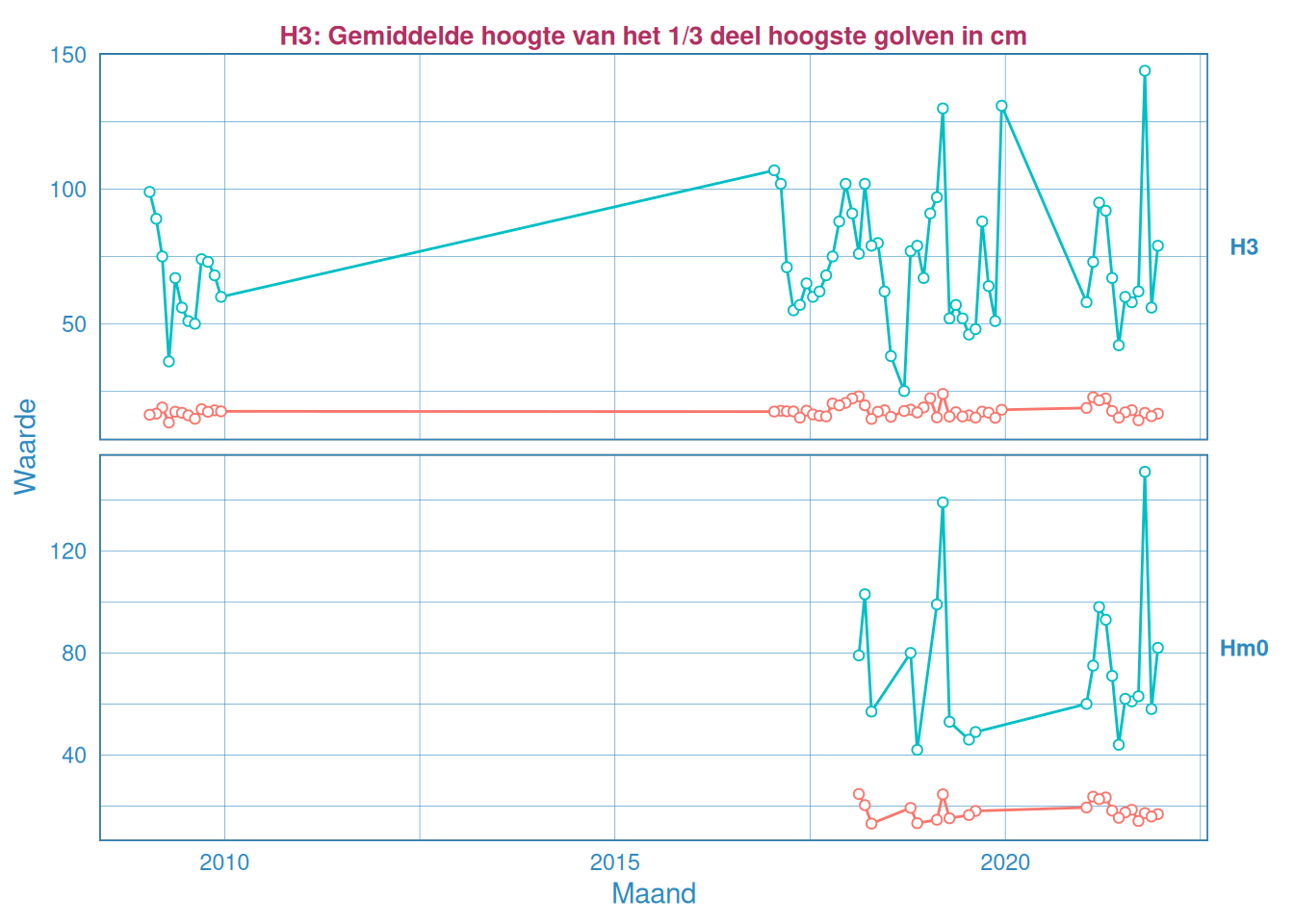
Figuur 2.36: Maandelijks gemiddelde en maximum van de significante golfhoogte \(H_{1/3}\) (boven) en \(H_{m0}\) (onder) voor station Pas van Terneuzen.
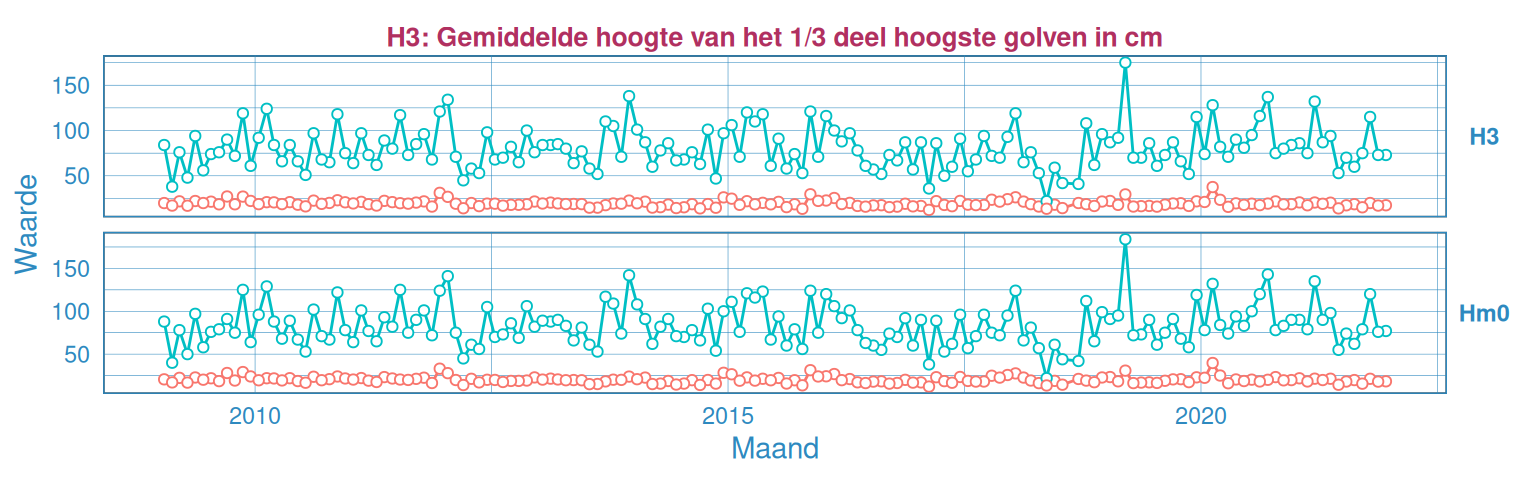
Figuur 2.37: Maandelijks gemiddelde en maximum van de significante golfhoogte \(H_{m0}\) voor station Overloop van Hansweert (Hier is geen H3 beschikbaar).
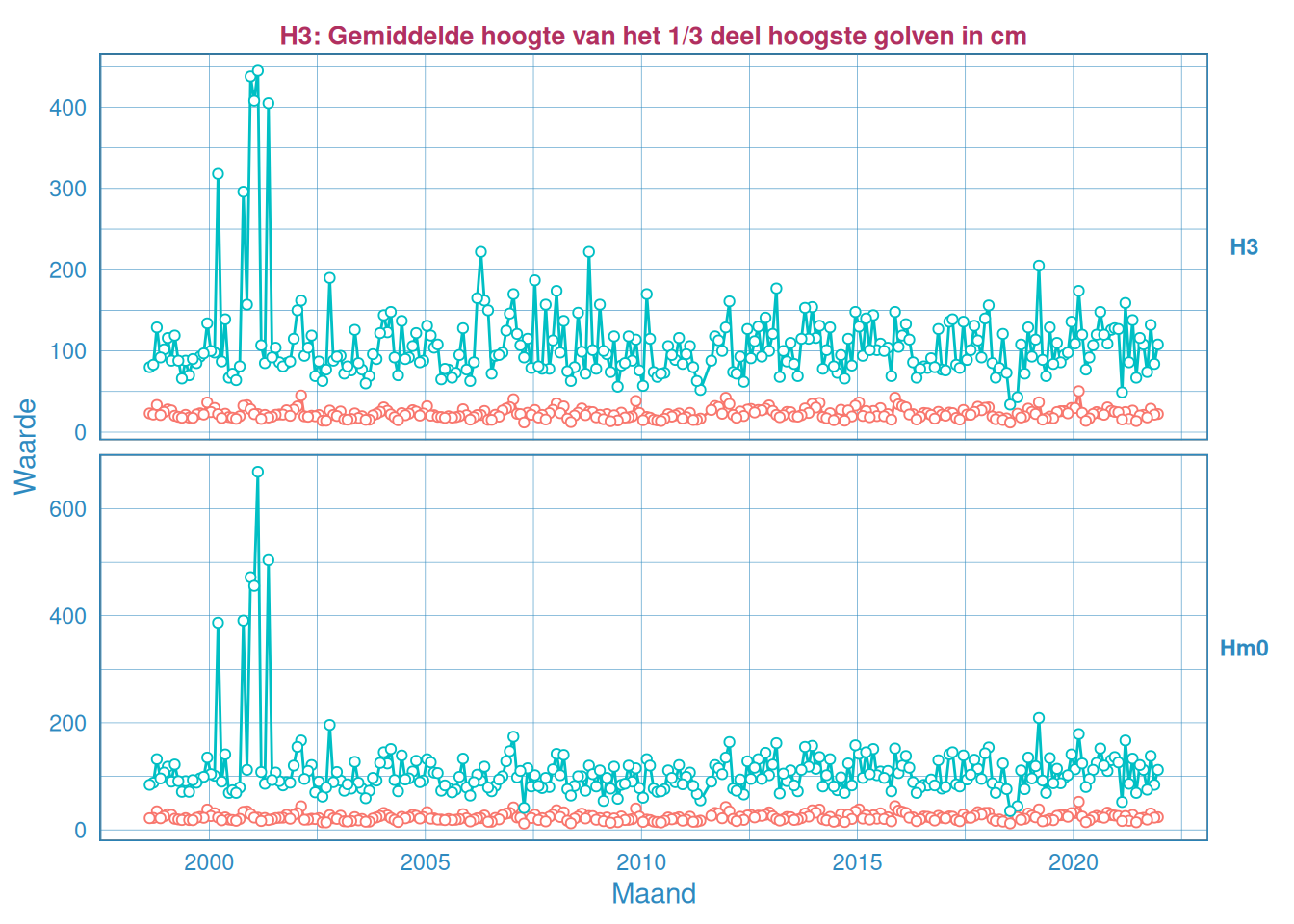
Figuur 2.38: Maandelijks gemiddelde en maximum van de significante golfhoogte \(H_{1/3}\) (boven) en \(H_{m0}\) (onder) voor station Hansweert.
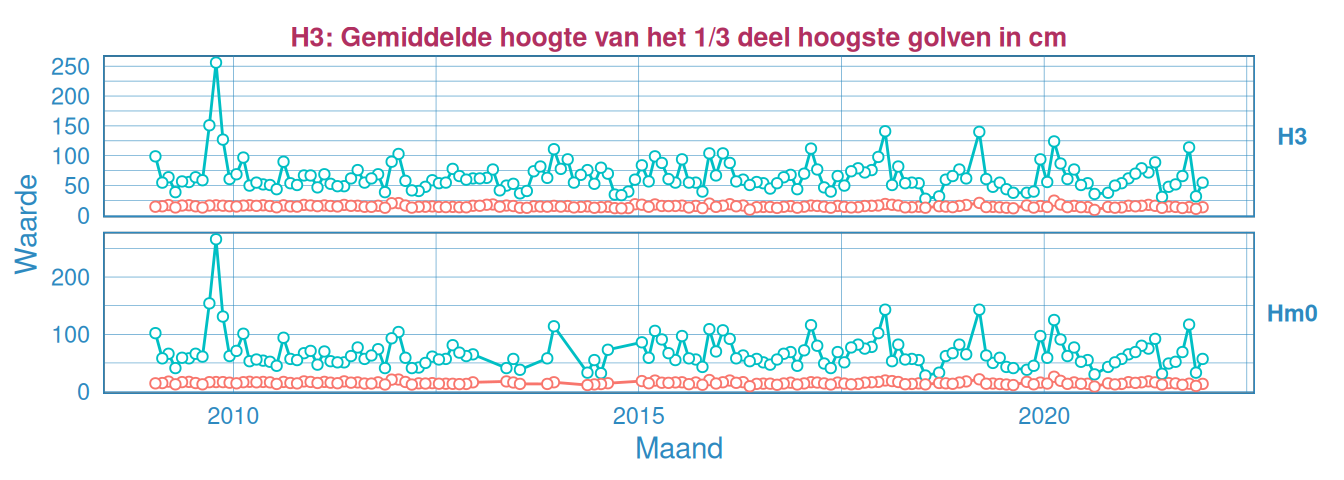
Figuur 2.39: Maandelijks gemiddelde en maximum van de significante golfhoogte \(H_{1/3}\) voor station Overloop van Valkenisse (Hm0 is hier niet beschikbaar.
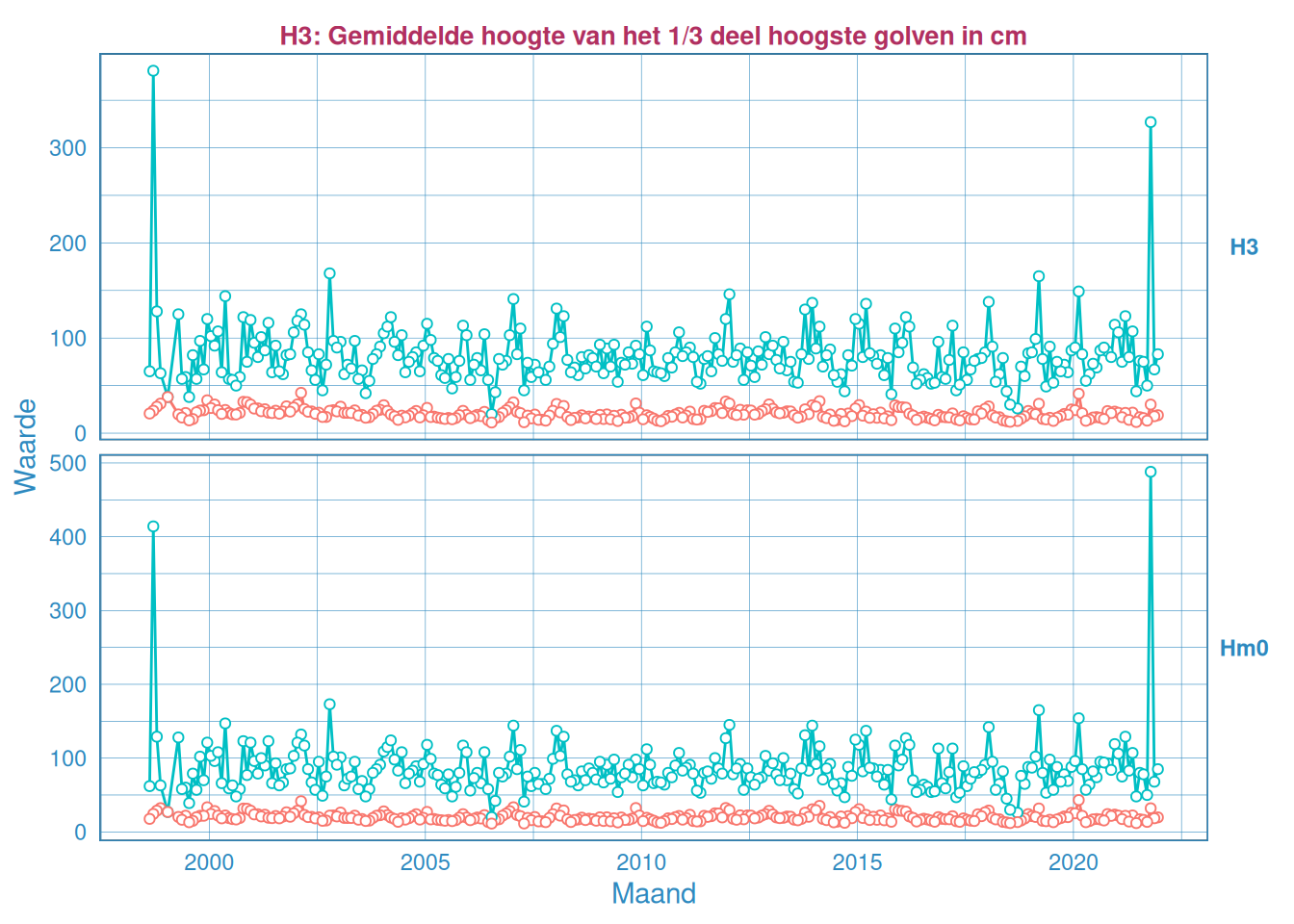
Figuur 2.40: Maandelijks gemiddelde en maximum van de significante golfhoogte \(H_{1/3}\) (boven) en \(H_{m0}\) (onder) voor station Bath.
2.2.3 Golfperiode
De golfperiode wordt weergegeven met twee parameters: \(T_{H,1/3}\) (de gemiddelde periode van de golven behorende bij de significante golfhoogte \(H_{1/3}\)) en \(T_{m02}\) (de gemiddelde periode van alle golven). De maandelijkse gemiddelden en maandelijkse maxima van de golfperiode zijn weergegeven in Figuur 2.43 t/m Figuur 2.52 voor \(T_{H,1/3}\) (telkens bovenste figuur) en \(T_{m02}\) (telkens onderste figuur). De meetstations zijn gerangschikt in stroomopwaartse richting. Voor maanden met een kwart of meer aan missende data worden de gemiddeldes met dunnere en transparante kleuren weergegeven. Aan deze gemiddeldes kan minder waarde gehecht worden.
De golfperiode \(T_{H,1/3}\) laat bij Hansweert en Bath een paar breuken in de meetreeksen zien, dit is waarschijnlijk te wijten aan meetgaten of \(-\)fouten. Op basis van de tijdseries per station constateren we geen trend in toe- of afname van de golfperiode. Wel opvallend dat de golfperiode \(T_{H,1/3}\) sinds 2015 voor de meeste stations langer is dan in 2014. Er is geen voor de hand liggende verklaring voor deze observatie.
De gemiddelde golfperiode behorende bij het hoogste 1/3 deel van de golven is duidelijk anders dan de gemiddelde golfperiode uit het spectrum, waarbij het spectrale gemiddelde van het kwadraat van de frequentie van alle golven is bepaald. %alle golven worden meegenomen. Hogere golven hebben een langere periode, zoals blijkt het verschil tussen \(T_{H,1/3}\) en \(T_{m02}\). Vooral in de Westerschelde is het verschil tussen de twee periodeparameters groot. Mogelijk speelt een rol dat \(T_{H,1/3}\) gedomineerd wordt door niet-lokaal opgewekte golven, en \(T_{m02}\) door kortere lokaal opgewekte golven. Er is geen voor de hand liggende reden hiervoor te noemen. Voor beide periodeparameters geldt dat de golven in de monding de langste periode hebben, zoals te zien in Figuur 2.41. De maximale gemiddelde golfperiode van lokaal opgewekte golven in de Westerschelde wordt, op basis van Breugem and Holthuijsen (2006), geschat op 4,3 seconden. Dit is gebaseerd op een strijklengte van 10 kilometer met een wind snelheid van 22 m/s. Voor stations op de Noordzee loopt de maximale golfperiode op tot +/- 18 seconden (e.g. swell condities). Langere golfperiodes hoeven niet noodzakelijkerwijs incorrect te zijn, maar het is twijfelachtig dat golfperiodes van meer dan 15 s en soms zelfs 30 s aan windgolven toe te schrijven, zeker als die op slechts op één locatie tegelijk optreden. Het is goed mogelijk dat de waarnemingen als bij Hansweert (Figuur 2.50) samenhangen met scheepsgolven of met effect van een schip dat voorbij komt.
Figuur 2.42 laat de empirische distributie van gemiddelde golfperiode op basis van alle beschikbare data zien. Hierin constateren we dat de mediaan van de golfperiode in de Westerschelde tussen de 3 en 4,5 seconden ligt. Algemeen geldt dat golven in de monding golfperiodes van 3-4 seconden hebben. In de Westerschelde neemt dit af en zijn er golf periodes van 1,5 tot 3 seconden. Opvallend is dat verschillende curves suggereren dat er een duidelijke knik zit bij ongeveer 3.5-4 seconden. Dit suggereert dat het mogelijk moet zijn, via spectrale filtering, om de scheepsgolven en de windgolven van elkaar te scheiden. Dat zou interessante informatie zijn, bijvoorbeeld bij het bepalen van de dijkhoogtes (er zijn geen scheepsgolven bij maatgevende condities).
| Station | Th3 med | Th3 max | Tm02 med | Tm02 max |
|---|---|---|---|---|
| Bath (BAT2) | 4.5 | 9.9 | 1.9 | 3.0 |
| Hansweert (HAWI) | 3.5 | 6.7 | 2.0 | 2.2 |
| Cadzand (CAWI) | 4.6 | 6.1 | 3.0 | 3.6 |
| Cadzand (CADW) | 4.5 | 5.6 | 3.7 | 4.6 |
| Overloop van Hansweert (OVHW) | 3.5 | 4.9 | 2.1 | 2.9 |
| Deurloo (DEUR) | 4.7 | 5.7 | 3.8 | 4.4 |
| Honte (HNTE) | 3.9 | 4.1 | 2.6 | 3.4 |
| Hoofdplaat (HFPL) | 3.9 | 7.0 | 1.6 | 1.8 |
| Overloop van Valkenisse (OVVA) | 3.8 | 4.2 | 2.4 | 2.7 |
| Pas van Terneuzen (PVT) | 3.6 | 3.7 | 2.2 | 2.3 |
| Wielingen (WIEL) | 4.2 | 5.9 | 3.1 | 4.3 |
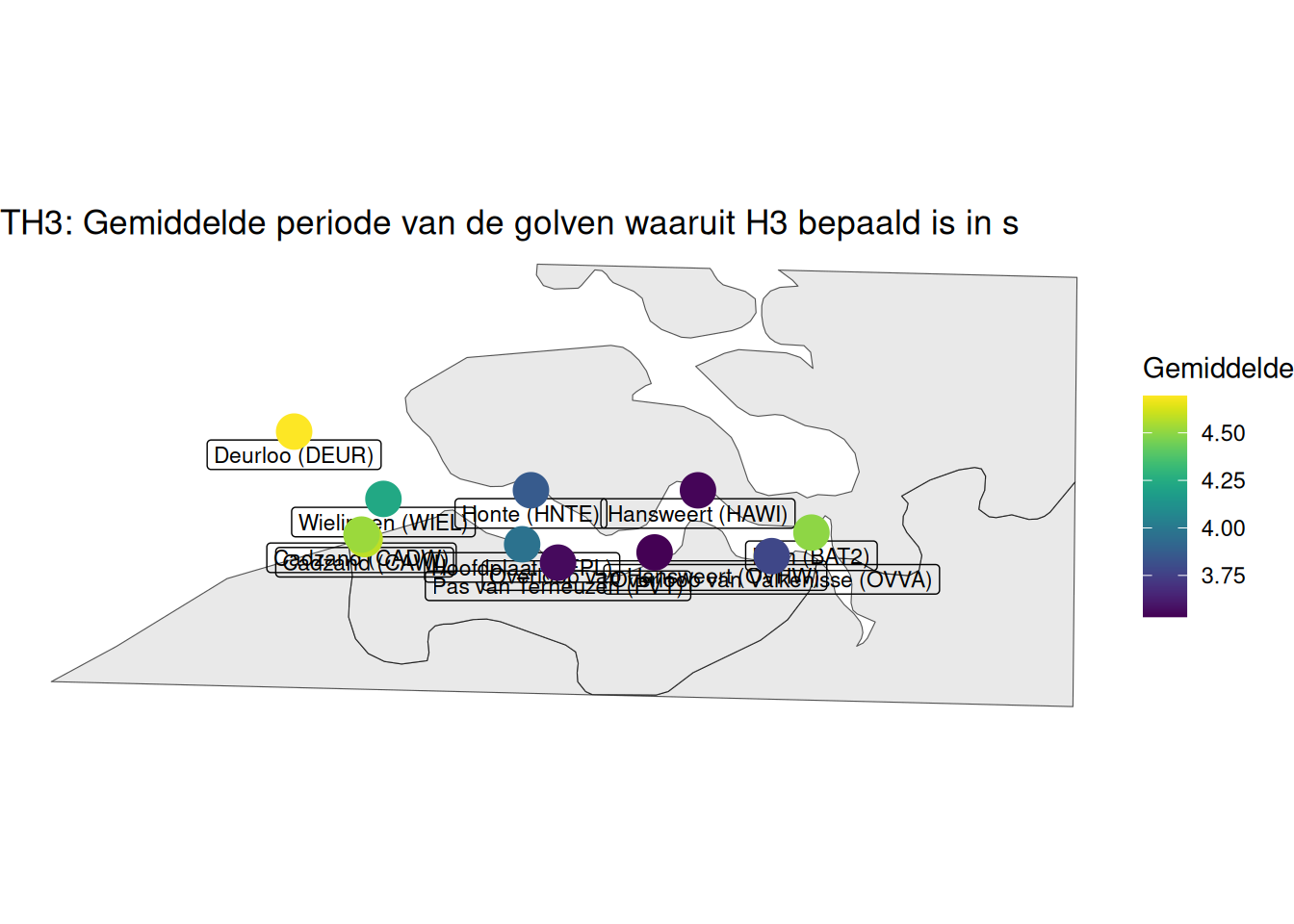
Figuur 2.41: Gewogen gemiddelde significante golfperiode per station berekend op basis van het spectrum voor alle beschikbare data vanaf 1998.
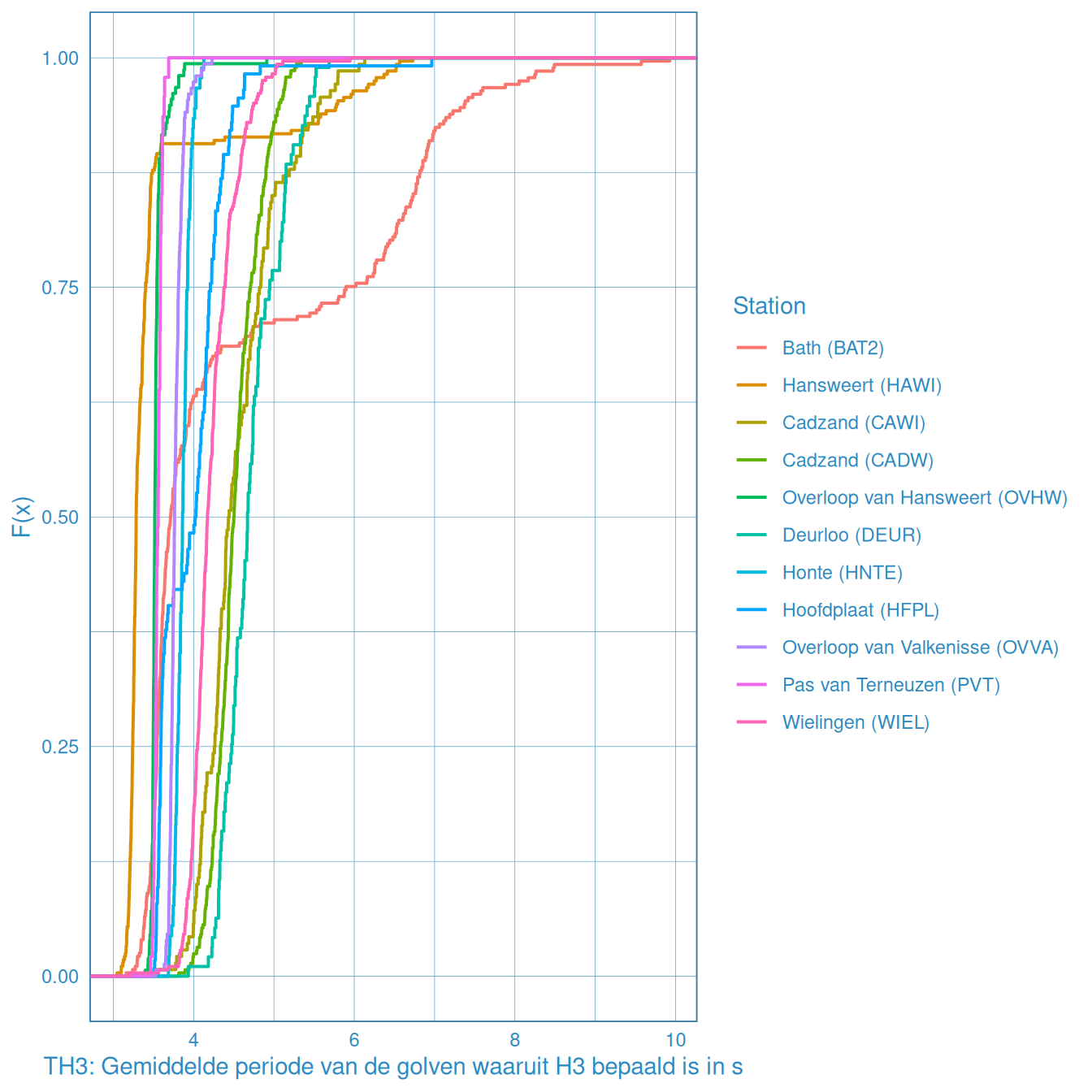
Figuur 2.42: Empirische distributiefunctie voor de significante golfperiode berekend op basis van het spectrum voor alle beschikbare data vanaf 1998.
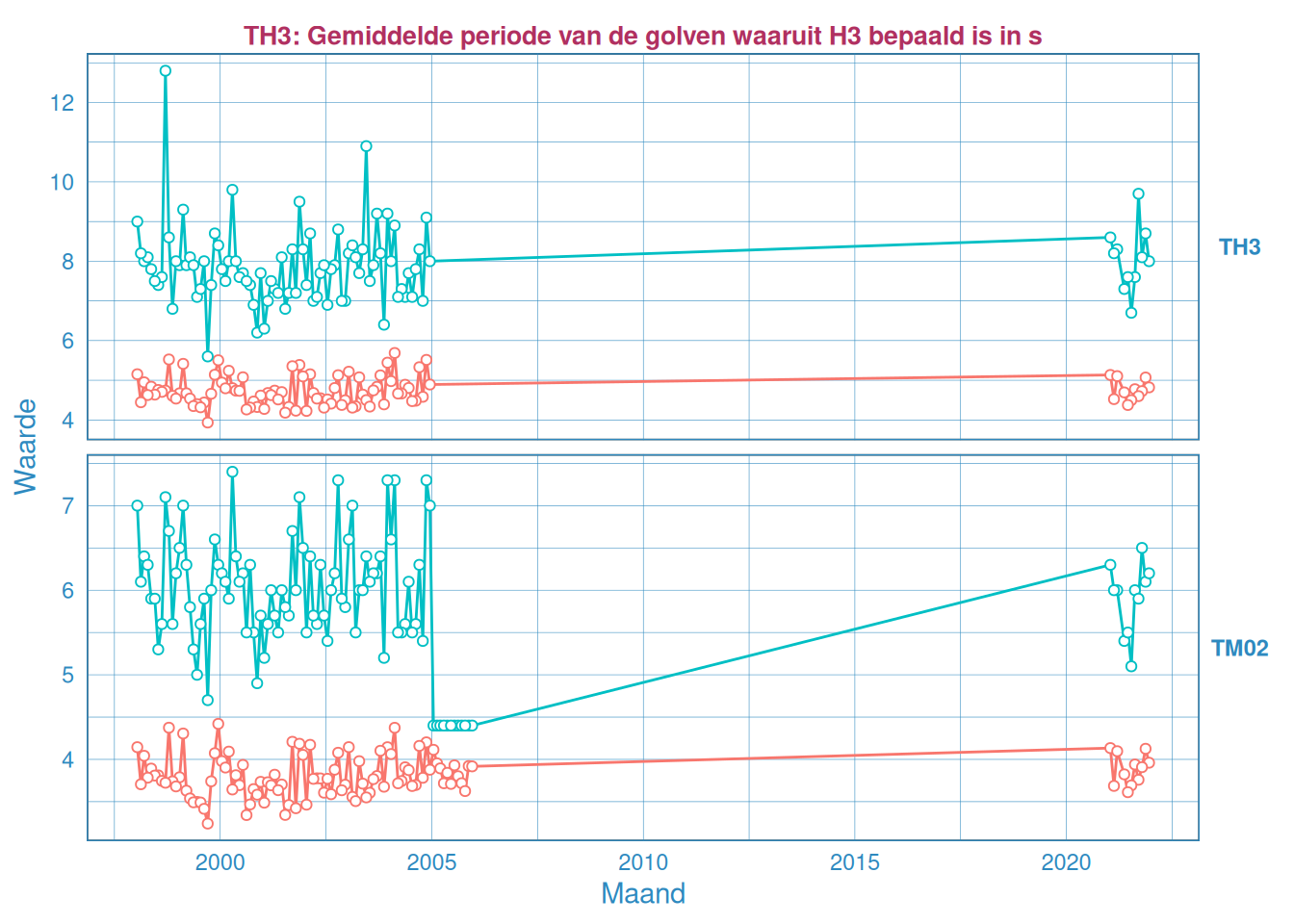
Figuur 2.43: Maandelijks gemiddelde (rood) en maximum (blauw) van de golfperiode \(T_{H 1/3}\) (boven) en \(T_{M02}\) (onder) voor station Deurloo.
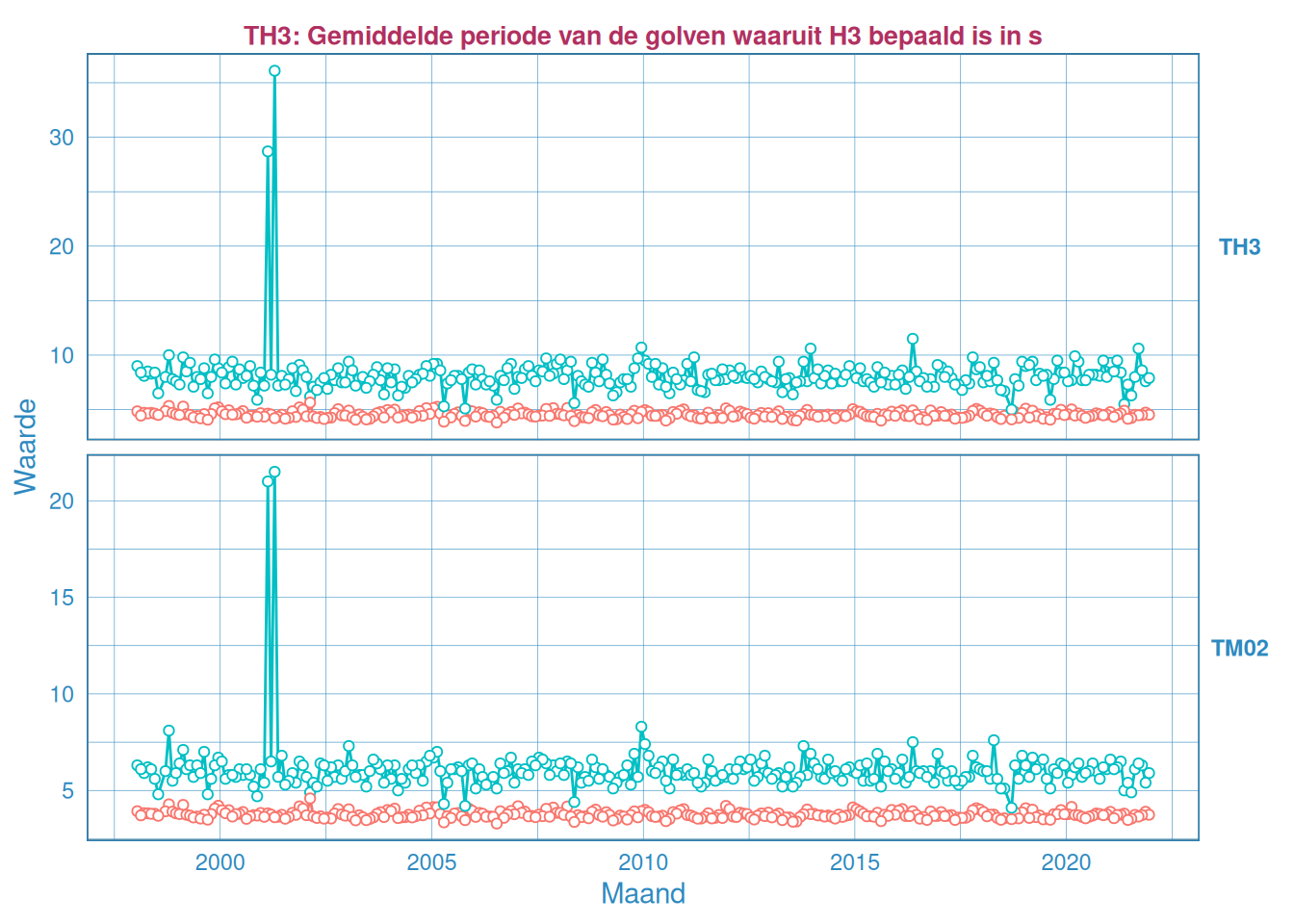
Figuur 2.44: Maandelijks gemiddelde en maximum van de golfperiode \(T_{H 1/3}\) (boven) en \(T_{M02}\) (onder) voor station Cadzand.
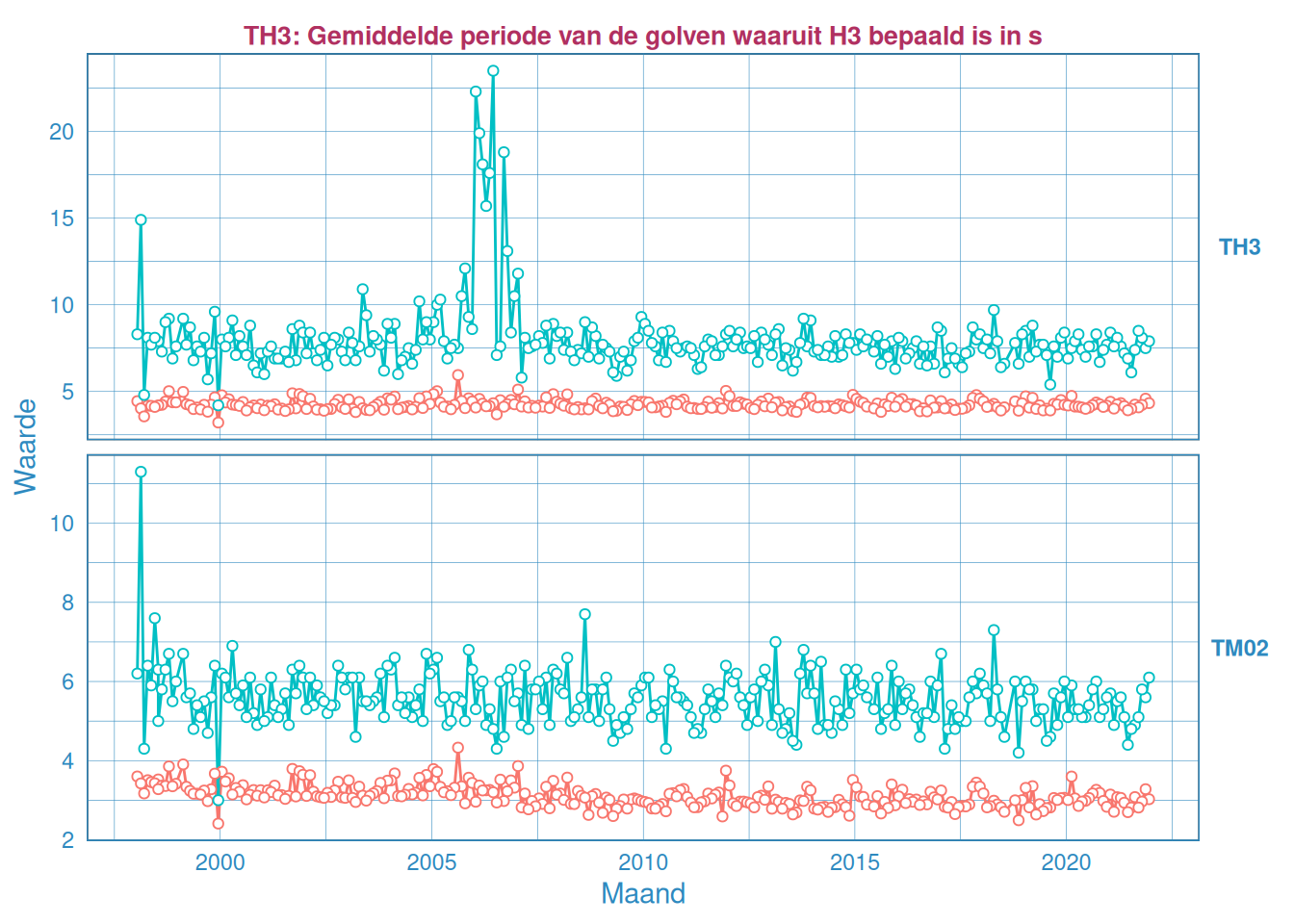
Figuur 2.45: Maandelijks gemiddelde en maximum van de golfperiode \(T_{H 1/3}\) (boven) en \(T_{M02}\) (onder) voor station Wielingen.
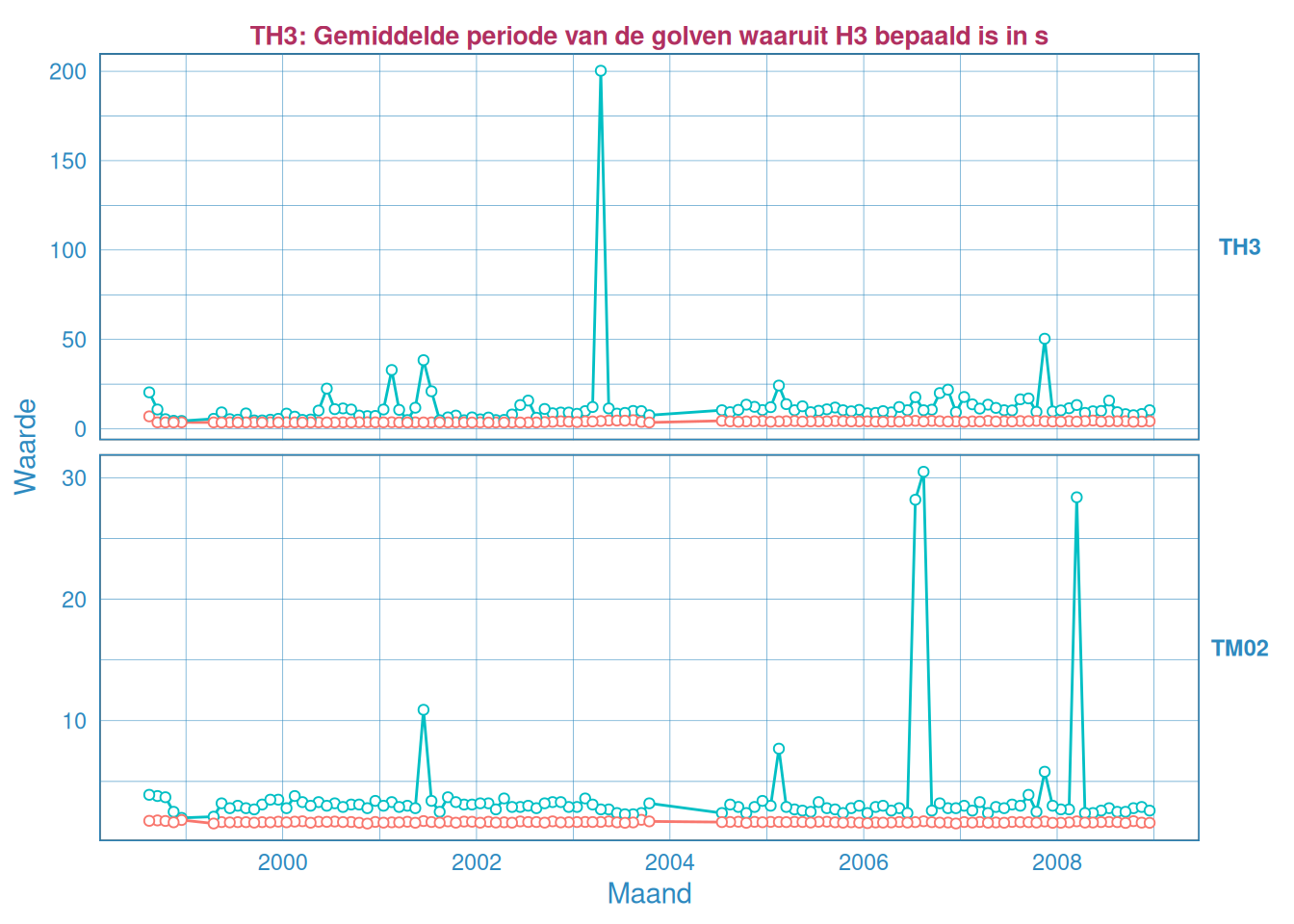
Figuur 2.46: Maandelijks gemiddelde en maximum van de golfperiode \(T_{H 1/3}\) (boven) en \(T_{M02}\) (onder) voor station Hoofdplaat.
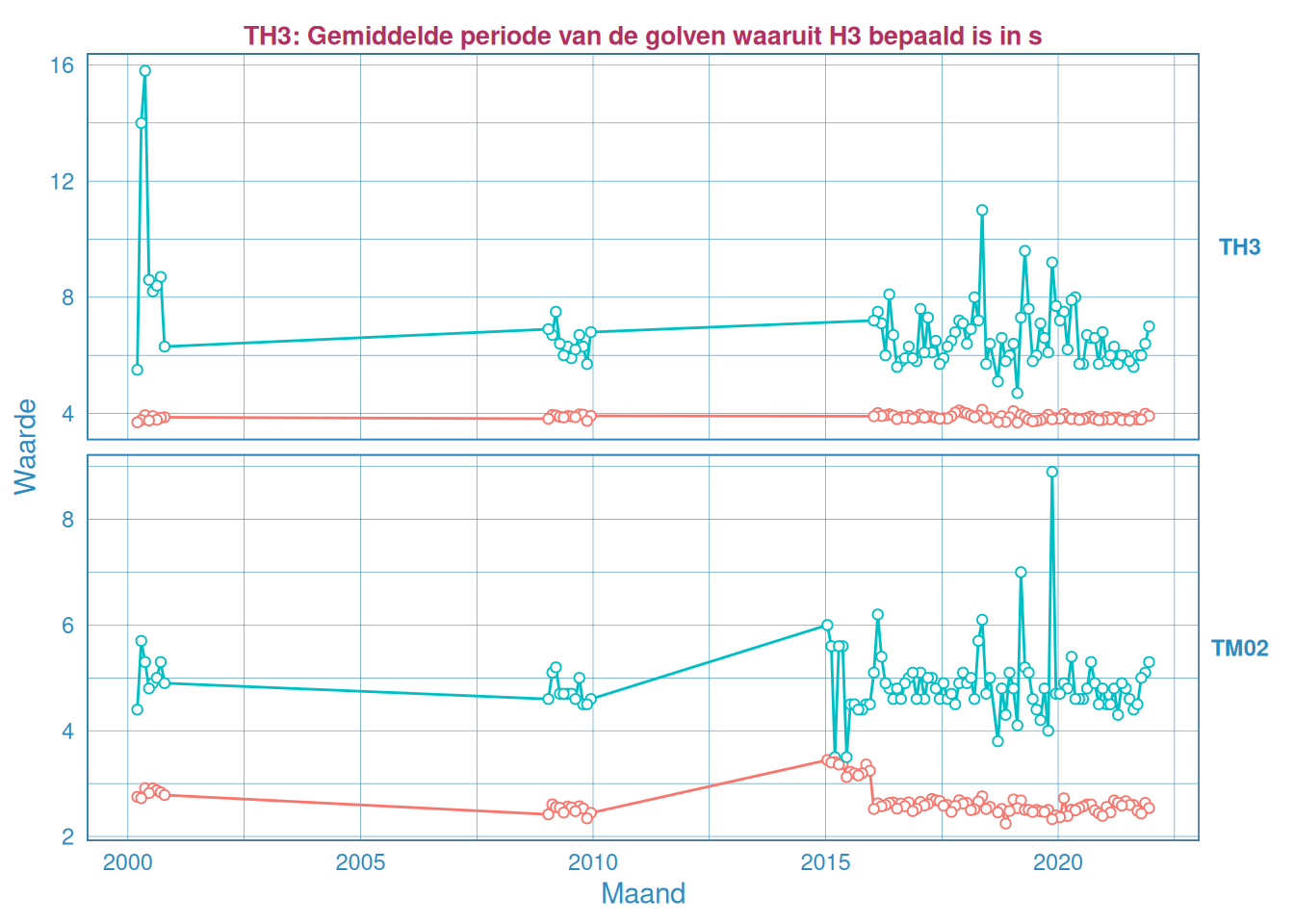
Figuur 2.47: Maandelijks gemiddelde en maximum van de golfperiode \(T_{H 1/3}\) (boven) en \(T_{M02}\) (onder) voor station Honte.
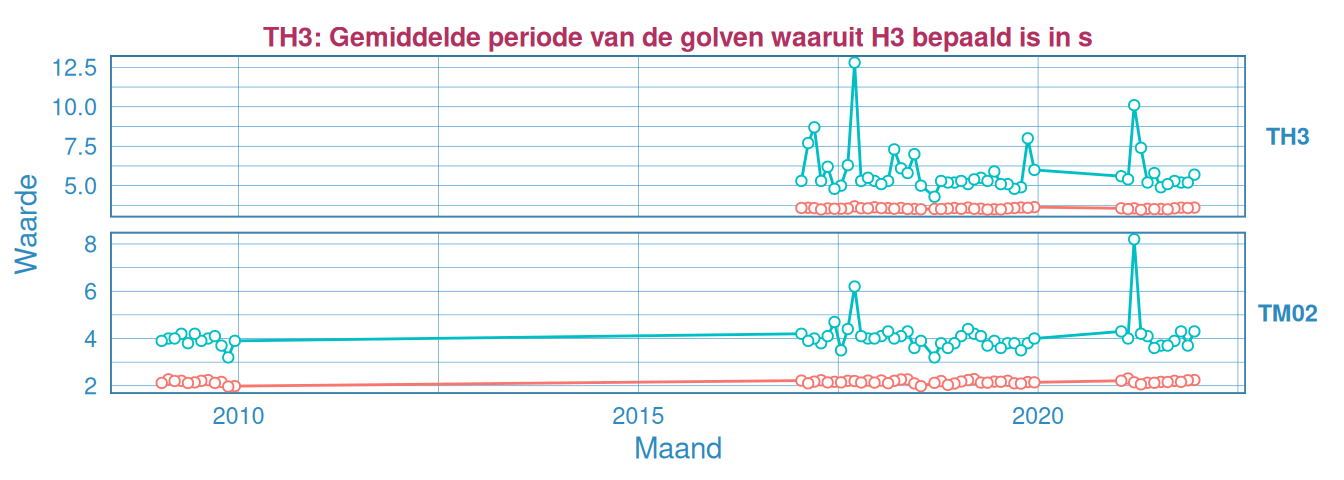
Figuur 2.48: Maandelijks gemiddelde en maximum van de golfperiode \(T_{H 1/3}\) (boven) en \(T_{M02}\) (onder) voor station Pas van Terneuzen.
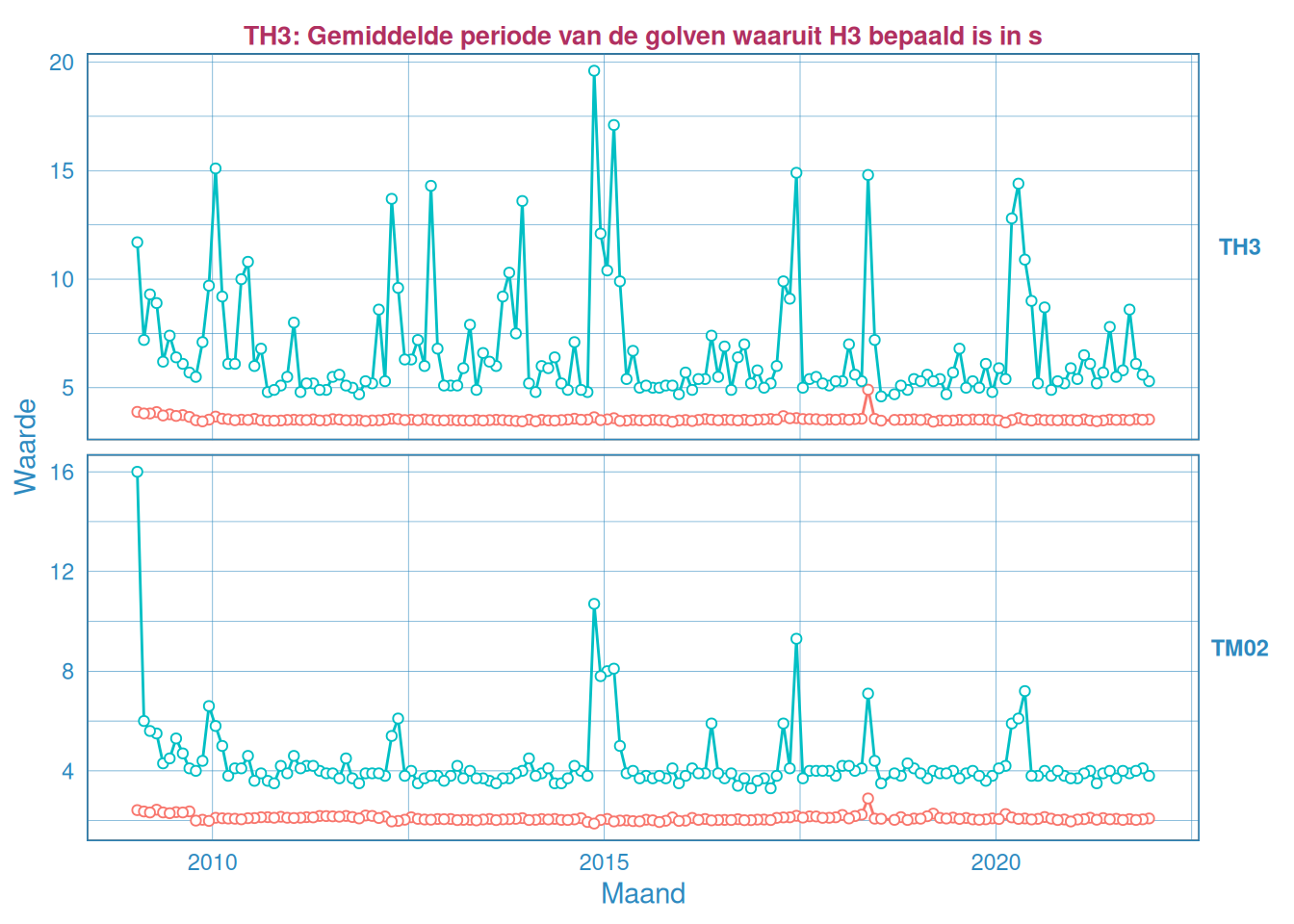
Figuur 2.49: Maandelijks gemiddelde en maximum van de golfperiode \(T_{H 1/3}\) (boven) en \(T_{M02}\) (onder) voor station Overloop van Hansweert.
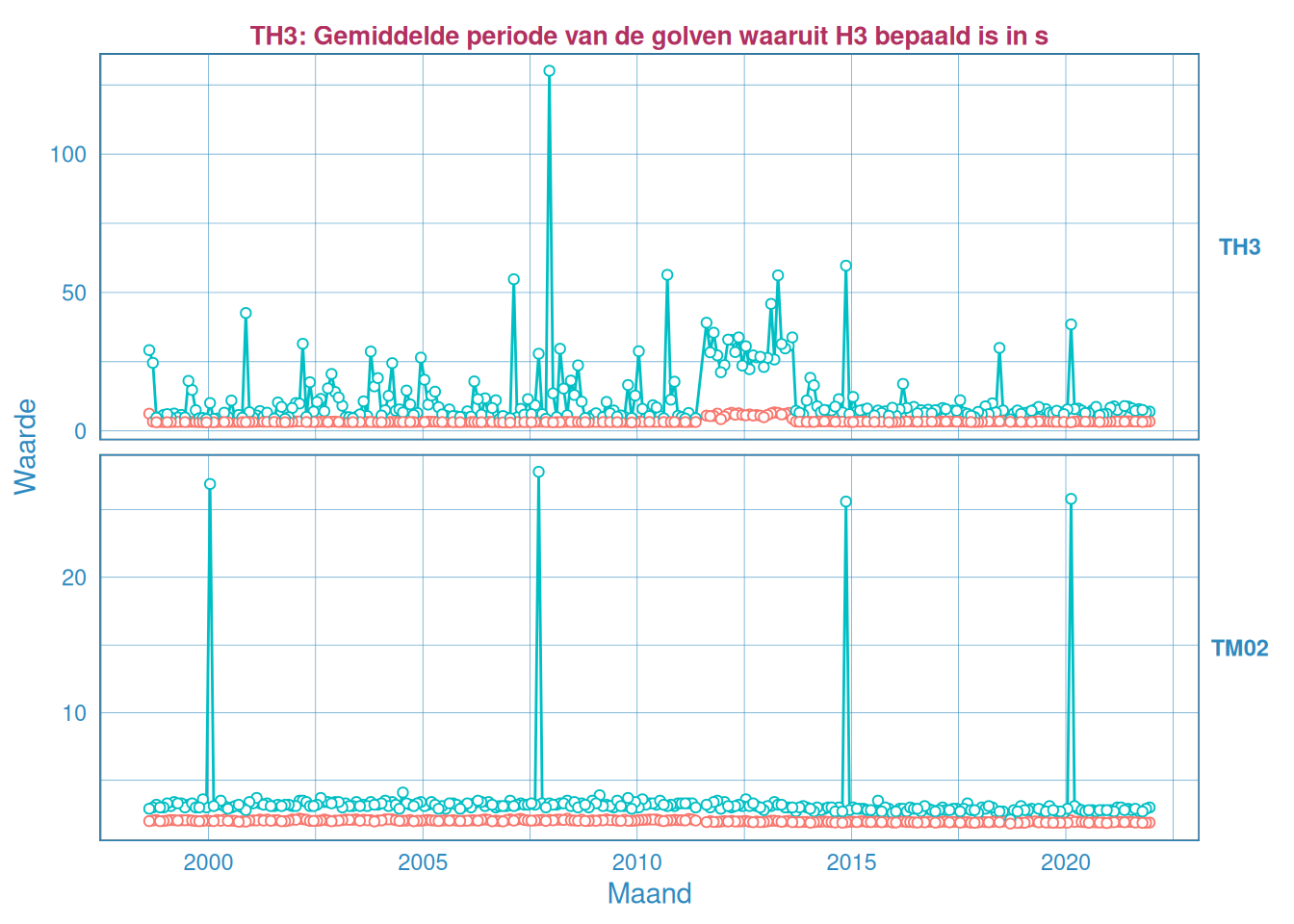
Figuur 2.50: Maandelijks gemiddelde en maximum van de golfperiode \(T_{H 1/3}\) (boven) en \(T_{M02}\) (onder) voor station Hansweert.
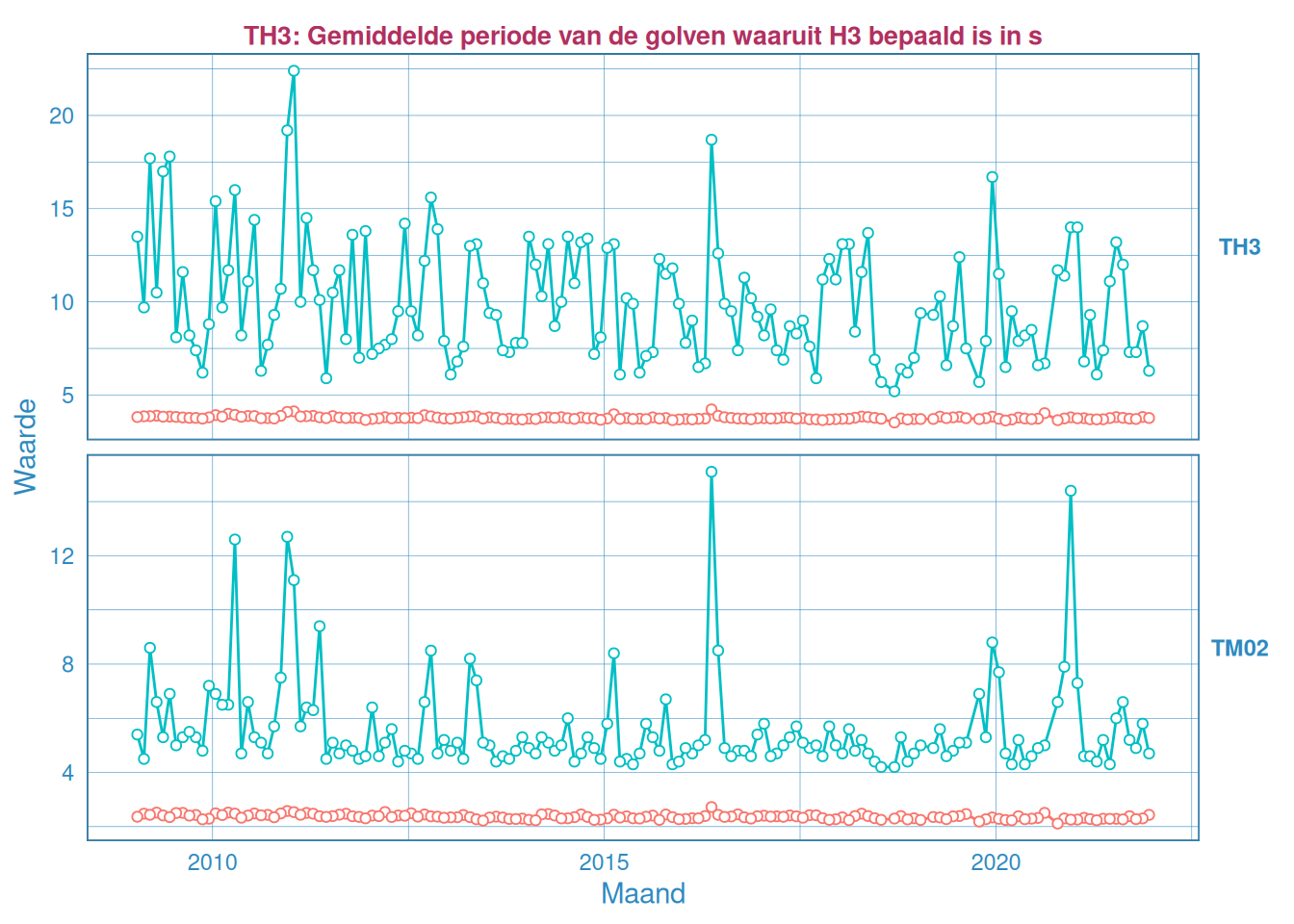
Figuur 2.51: Maandelijks gemiddelde en maximum van de golfperiode \(T_{H 1/3}\) (boven) en \(T_{M02}\) (onder) voor station Overloop van Valkenisse.
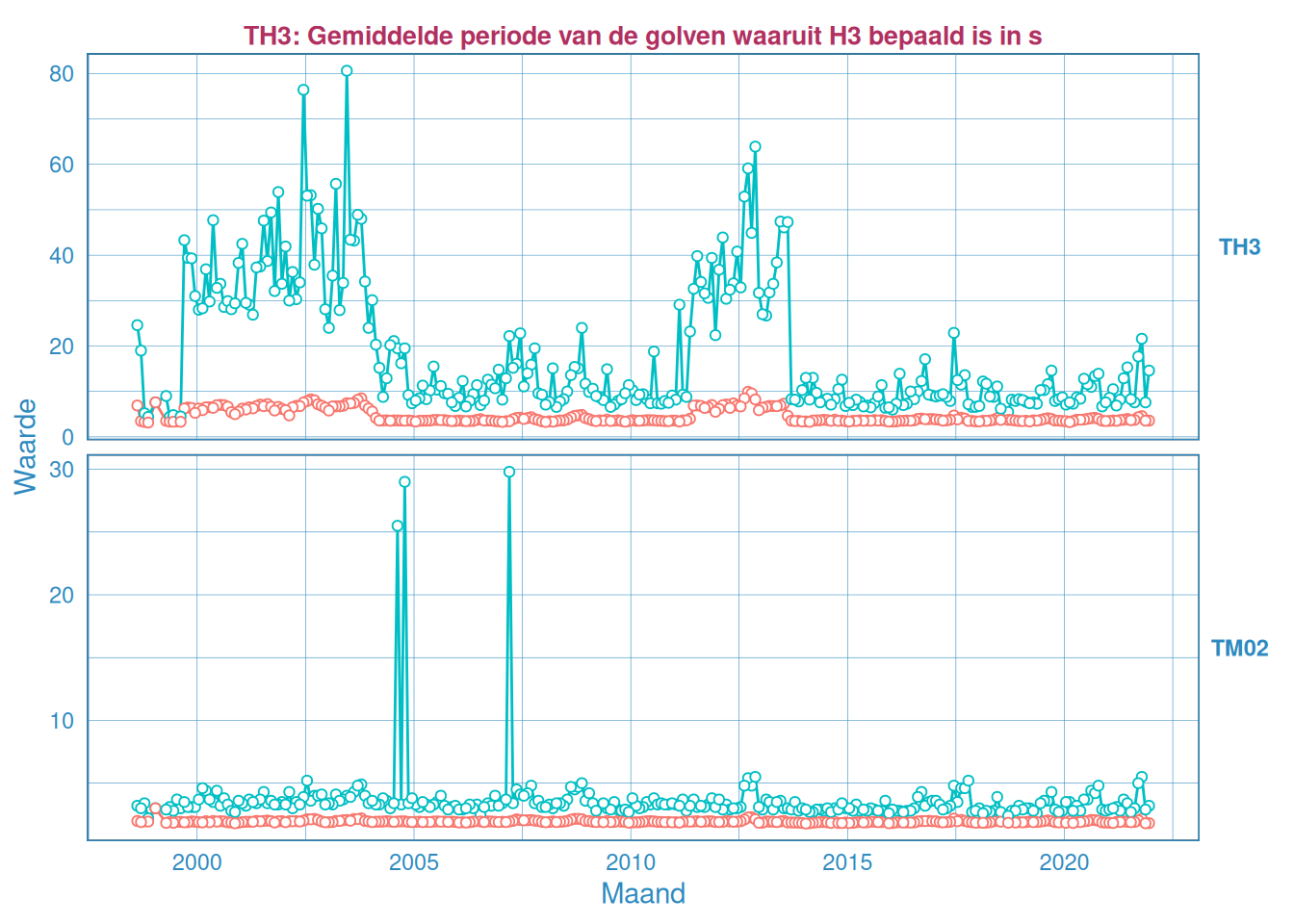
Figuur 2.52: Maandelijks gemiddelde en maximum van de golfperiode \(T_{H 1/3}\) (boven) en \(T_{M02}\) (onder) voor station Bath.